Cell lineages and the logic of proliferative control
- PMID: 19166268
- PMCID: PMC2628408
- DOI: 10.1371/journal.pbio.1000015
Cell lineages and the logic of proliferative control
Abstract
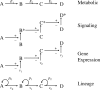
It is widely accepted that the growth and regeneration of tissues and organs is tightly controlled. Although experimental studies are beginning to reveal molecular mechanisms underlying such control, there is still very little known about the control strategies themselves. Here, we consider how secreted negative feedback factors ("chalones") may be used to control the output of multistage cell lineages, as exemplified by the actions of GDF11 and activin in a self-renewing neural tissue, the mammalian olfactory epithelium (OE). We begin by specifying performance objectives-what, precisely, is being controlled, and to what degree-and go on to calculate how well different types of feedback configurations, feedback sensitivities, and tissue architectures achieve control. Ultimately, we show that many features of the OE-the number of feedback loops, the cellular processes targeted by feedback, even the location of progenitor cells within the tissue-fit with expectations for the best possible control. In so doing, we also show that certain distinctions that are commonly drawn among cells and molecules-such as whether a cell is a stem cell or transit-amplifying cell, or whether a molecule is a growth inhibitor or stimulator-may be the consequences of control, and not a reflection of intrinsic differences in cellular or molecular character.
Conflict of interest statement
Competing interests. The authors have declared that no competing interests exist.
Figures



Comment in
-
Biological systems from an engineer's point of view.PLoS Biol. 2009 Jan 20;7(1):e21. doi: 10.1371/journal.pbio.1000021. PLoS Biol. 2009. PMID: 19166272 Free PMC article.
Similar articles
-
Activin and GDF11 collaborate in feedback control of neuroepithelial stem cell proliferation and fate.Development. 2011 Oct;138(19):4131-42. doi: 10.1242/dev.065870. Epub 2011 Aug 18. Development. 2011. PMID: 21852401 Free PMC article.
-
Feedback regulation in multistage cell lineages.Math Biosci Eng. 2009 Jan;6(1):59-82. doi: 10.3934/mbe.2009.6.59. Math Biosci Eng. 2009. PMID: 19292508 Free PMC article.
-
Autoregulation of neurogenesis by GDF11.Neuron. 2003 Jan 23;37(2):197-207. doi: 10.1016/s0896-6273(02)01172-8. Neuron. 2003. PMID: 12546816
-
Identification and molecular regulation of neural stem cells in the olfactory epithelium.Exp Cell Res. 2005 Jun 10;306(2):309-16. doi: 10.1016/j.yexcr.2005.03.027. Epub 2005 Apr 21. Exp Cell Res. 2005. PMID: 15925585 Review.
-
Neurogenesis and cell death in olfactory epithelium.J Neurobiol. 1996 May;30(1):67-81. doi: 10.1002/(SICI)1097-4695(199605)30:1<67::AID-NEU7>3.0.CO;2-E. J Neurobiol. 1996. PMID: 8727984 Review.
Cited by
-
The role of cell location and spatial gradients in the evolutionary dynamics of colon and intestinal crypts.Biol Direct. 2016 Aug 23;11(1):42. doi: 10.1186/s13062-016-0141-6. Biol Direct. 2016. PMID: 27549762 Free PMC article.
-
Stem cells in the light of evolution.Indian J Med Res. 2012 Jun;135(6):813-9. Indian J Med Res. 2012. PMID: 22825600 Free PMC article. Review.
-
Stability analysis of a multiscale model of cell cycle dynamics coupled with quiescent and proliferating cell populations.PLoS One. 2023 Jan 20;18(1):e0280621. doi: 10.1371/journal.pone.0280621. eCollection 2023. PLoS One. 2023. PMID: 36662844 Free PMC article.
-
STOCHASTIC DYNAMICS OF CELL LINEAGE IN TISSUE HOMEOSTASIS.Discrete Continuous Dyn Syst Ser B. 2019 Aug;24(8):3971-3994. doi: 10.3934/dcdsb.2018339. Discrete Continuous Dyn Syst Ser B. 2019. PMID: 32269502 Free PMC article.
-
Foxg1 promotes olfactory neurogenesis by antagonizing Gdf11.Development. 2009 May;136(9):1453-64. doi: 10.1242/dev.034967. Epub 2009 Mar 18. Development. 2009. PMID: 19297409 Free PMC article.
References
-
- Stern CD, Fraser SE. Tracing the lineage of tracing cell lineages. Nat Cell Biol. 2001;3:E216–218. - PubMed
-
- Fichelson P, Audibert A, Simon F, Gho M. Cell cycle and cell-fate determination in Drosophila neural cell lineages. Trends Genet. 2005;21:413–420. - PubMed
-
- Iwasaki H, Akashi K. Myeloid lineage commitment from the hematopoietic stem cell. Immunity. 2007;26:726–740. - PubMed
-
- Shostak S. (Re)defining stem cells. Bioessays. 2006;28:301–308. - PubMed

