Covariate adjusted correlation analysis with application to FMR1 premutation female carrier data

Abstract

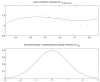
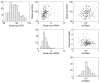
Motivated by molecular data on female premutation carriers of the fragile X mental retardation 1 (FMR1) gene, we present a new method of covariate adjusted correlation analysis to examine the association of messenger RNA (mRNA) and number of CGG repeat expansion in the FMR1 gene. The association between the molecular variables in female carriers needs to adjust for activation ratio (ActRatio), a measure which accounts for the protective effects of one normal X chromosome in females carriers. However, there are inherent uncertainties in the exact effects of ActRatio on the molecular measures of interest. To account for these uncertainties, we develop a flexible adjustment that accommodates both additive and multiplicative effects of ActRatio nonparametrically. The proposed adjusted correlation uses local conditional correlations, which are local method of moments estimators, to estimate the Pearson correlation between two variables adjusted for a third observable covariate. The local method of moments estimators are averaged to arrive at the final covariate adjusted correlation estimator, which is shown to be consistent. We also develop a test to check the nonparametric joint additive and multiplicative adjustment form. Simulation studies illustrate the efficacy of the proposed method. (Application to FMR1 premutation data on 165 female carriers indicates that the association between mRNA and CGG repeat after adjusting for ActRatio is stronger.) Finally, the results provide independent support for a specific jointly additive and multiplicative adjustment form for ActRatio previously proposed in the literature.

Figure 1

(Top panel) Scatter plot of the local correlation estimates r_j versus ${\text{U}}_J^M$ for j = 1,…, 20 bins, with approximately eight points per bin. A local linear smooth overlays the scatterplot with an automatically selected bandwidth of h = 0.1. (Bottom panel) Plot of the estimated nonparametric density (dashed line) of 1000 standardized bootstrap estimates used in forming the 95% CIs for ρ_mRNA,CGG in the data application. The standard normal density (solid line) is also given.

Figure 2

(Top panel) Plots of ρ̃(u) from the two cases of alternatives to the proposed additive and multiplicative distortion form. The null hypothesis of additive and multiplicative forms corresponds to θ = 0, i.e., the (conditional) correlation function ρ̃(u) is constant. Increasing deviation away from the null is parameterized by θ = 1,…, 8. (Bottom panel) Power curves for the two cases of alternatives/deviations at significance levels α = 0.05 (bottom curve of same line type) and 0.10 for n = 150 (dotted curves), n = 300 (solid curves), and n = 600 (dash-dotted curves).

Figure 3

Matrix plot of the observed variables $\stackrel{\sim }{\text{CGG}}$, $\stackrel{\sim }{\text{mRNA}}$, and ActRatio for n = 165 female premutation carriers.