Three-dimensional linear system analysis for breast tomosynthesis
- PMID: 19175081
- PMCID: PMC2673606
- DOI: 10.1118/1.2996014
Three-dimensional linear system analysis for breast tomosynthesis
Abstract
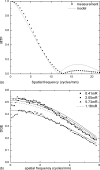
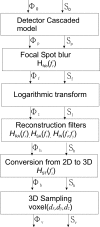
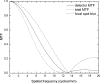
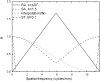
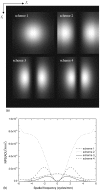
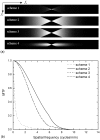
The optimization of digital breast tomosynthesis (DBT) geometry and reconstruction is crucial for the clinical translation of this exciting new imaging technique. In the present work, the authors developed a three-dimensional (3D) cascaded linear system model for DBT to investigate the effects of detector performance, imaging geometry, and image reconstruction algorithm on the reconstructed image quality. The characteristics of a prototype DBT system equipped with an amorphous selenium flat-panel detector and filtered backprojection reconstruction were used as an example in the implementation of the linear system model. The propagation of signal and noise in the frequency domain was divided into six cascaded stages incorporating the detector performance, imaging geometry, and reconstruction filters. The reconstructed tomosynthesis imaging quality was characterized by spatial frequency dependent presampling modulation transfer function (MTF), noise power spectrum (NPS), and detective quantum efficiency (DQE) in 3D. The results showed that both MTF and NPS were affected by the angular range of the tomosynthesis scan and the reconstruction filters. For image planes parallel to the detector (in-plane), MTF at low frequencies was improved with increase in angular range. The shape of the NPS was affected by the reconstruction filters. Noise aliasing in 3D could be introduced by insufficient voxel sampling, especially in the z (slice-thickness) direction where the sampling distance (slice thickness) could be more than ten times that for in-plane images. Aliasing increases the noise at high frequencies, which causes degradation in DQE. Application of a reconstruction filter that limits the frequency components beyond the Nyquist frequency in the z direction, referred to as the slice thickness filter, eliminates noise aliasing and improves 3D DQE. The focal spot blur, which arises from continuous tube travel during tomosynthesis acquisition, could degrade DQE significantly because it introduces correlation in signal only, not NPS.
Figures
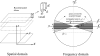







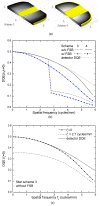
References
-
- Wu T., Moore R. H., Elizabeth A. B., Rafferty A., and Kopans D. B., in Categorical Courses in Diagnostic Radiology Physics: Advances in Breast Imaging: Physics, Technology, and Clinical Applications, edited by Karellas Andrew and Giger Maryellen L. (2004), pp. 149–165.
-
- Ren B. et al. , “Design and performance of the prototype full field breast tomosynthesis system with selenium based flat panel detector,” Proc. SPIE PSISDG10.1117/12.595833 5745, 550–561 (2005). - DOI
-
- Bissonnette M. et al. , “Digital breast tomosynthesis using an amorphous selenium flat panel detector,” Proc. SPIE PSISDG10.1117/12.601622 5745, 529–540 (2005). - DOI
-
- Mertelmeier T., Orman J., Haerer W., and Dudam M. K., “Optimizing filtered backprojection reconstruction for a breast tomosynthesis prototype device,” Proc. SPIE PSISDG10.1117/12.651380 6142, 61420F (2006). - DOI
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Miscellaneous

