Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2008 Dec;35(12):5242-52.
doi: 10.1118/1.2996110.

Image artifacts in digital breast tomosynthesis: investigation of the effects of system geometry and reconstruction parameters using a linear system approach

Yue-Houng Hu  1 , Bo Zhao, Wei Zhao
Affiliations

Image artifacts in digital breast tomosynthesis: investigation of the effects of system geometry and reconstruction parameters using a linear system approach

Yue-Houng Hu et al. Med Phys. 2008 Dec.

Abstract

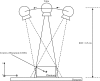
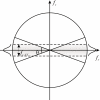
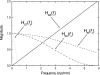
Digital breast tomosynthesis (DBT) is a three-dimensional (3D) x-ray imaging modality that reconstructs image slices parallel to the detector plane. Image acquisition is performed using a limited angular range (less than 50 degrees) and a limited number of projection views (less than 50 views). Due to incomplete data sampling, image artifacts are unavoidable in DBT. In this preliminary study, the image artifacts in DBT were investigated systematically using a linear system approximation. A cascaded linear system model of DBT was developed to calculate the 3D presampling modulation transfer function (MTF) with different image acquisition geometries and reconstruction filters using a filtered backprojection (FBP) algorithm. A thin, slanted tungsten (W) wire was used to measure the presampling MTF of the DBT system in the cross-sectional plane defined by the thickness (z-) and tube travel (x-) directions. The measurement was in excellent agreement with the calculation using the model. A small steel bead was used to calculate the artifact spread function (ASF) of the DBT system. The ASF was correlated with the convolution of the two-dimensional (2D) point spread function (PSF) of the system and the object function of the bead. The results showed that the cascaded linear system model can be used to predict the magnitude of image artifacts of small, high-contrast objects with different image acquisition geometry and reconstruction filters.

PubMed Disclaimer

Figures

Figure 1
Figure 1
The experimental DBT unit operates under partial isocentric motion with a stationary detector. The x-ray tube travels along an arc in the x-z plane with an angular range of ±25 degrees.
Figure 2
Figure 2
DBT acquires images over a limited angular range. The sampled region in the frequency domain is in the shape of a double wedge with angle θ. The effect of the slice-thickness filter is highlighted with gradient shading.
Figure 3
Figure 3
The reconstruction filter functions in their corresponding spatial frequency directions. The RA filter, HRA, is given as a function of fx and fz, the SA filter, HSA, is given as a function of fx, and the slice thickness filter, HST, is given as a function of fz. The interpolation filter, HIN, is plotted as a function of fx however; in two dimensions it is a function of both fx and fy.
Figure 4
Figure 4
A tungsten wire phantom is used to image a 2D point spread function (PSF). The wire is tilted at an angle, β, with respect to the z-axis and oriented orthogonally to the direction of tube motion.
Figure 5
Figure 5
The in-plane (x-y) image of a tilted W wire phantom reconstructed using simple backprojection (SBP). Both axes are in units of mm. The z-dependence of image intensity can be derived from the y-dependence using the angle of the wire and Eq. 7.
Figure 6
Figure 6
Flow chart showing the cascaded stages of the linear system model for calculating the 3D MTF of the DBT system. The left column shows the description of each stage, and the graphs on the right show conceptually the change in MTF after each cascaded stage.
Figure 7
Figure 7
Comparison between measured (left) and modeled (right) 2D PSF in the x-z plane. The graphs (a)–(d) correspond to filter schemes 1–4 listed in Table 1. The PSF in each graph is plotted from −4.85 to 4.85 mm along the x-direction, and −6 to 6 mm in the z-direction.
Figure 8
Figure 8
The comparison between measured and modeled 1D PSF in z-direction (with x=0). The graphs (a), (b), and (c) correspond to filter schemes 1, 3, and 4, respectively. Plot (d) is a comparison between the modeled 1D PSF in the z-direction for each filter scheme.
Figure 9
Figure 9
Comparison between the measured presampling PSF for the angular range of (from left to right): ±20, ±15, ±10, and ±5 degrees. The image reconstruction was performed using filter scheme 3.
Figure 10
Figure 10
The comparison between measured and modeled 1D PSF in the z-direction (x=0) with the angular range of (a) ±20 degrees; (b) ±15 degrees; (c) ±10 degrees; and (d) ±5 degrees. Filter scheme 3 was used in all cases.
Figure 11
Figure 11
Comparison of modeled 1D PSF in the z-direction (x=0) for the angular ranges of ±10, ±20, and ±30 degrees. All results were modeled using filter scheme 3.
Figure 12
Figure 12
Stacked image slices showing the artifact of the steel bead as a function of their distance from the location of the bead. A small ROI with 11 image lines was selected from each slice to include the entire image or artifact of the bead. Images (a)–(d) corresponded to reconstructions using filter schemes 1 to 4.
Figure 13
Figure 13
The stacked images∕artifacts of the bead with reconstruction using: (a) a limited angular range of ±5 degrees; and (b) a wider angular separation of 3.2 degrees with angular range of ±20 degrees. Filter scheme 3 was used in all cases.
Figure 14
Figure 14
Comparison between modeled and measured ASF: (a)–(d) correspond to filter schemes 1–4, respectively. The modeled ASF was calculated by multiplying the signal spectrum of a 0.4 mm diameter sphere with the presampling MTF of the DBT system, followed by an inverse Fourier transform. The vertical line with x=0 was normalized and plotted as the modeled ASF.
Figure 15
Figure 15
Comparison of ASF with different acquisition geometries: 49 views over ±20 degrees (solid line); 13 views over ±5 degrees (squares); and 13 views over ±20 degrees (triangles).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Laya M. B. et al. , “Effect of estrogen replacement therapy on the specificity and sensitivity of screening mammography,” J. Natl. Cancer Inst. JNCIEQ10.1093/jnci/88.10.643 88, 643–649 (1996). - DOI - PubMed
    1. Suryanarayanan S. et al. , “Evaluation of linear and nonlinear tomosynthetic reconstruction methods in digital mammography,” Acad. Radiol. ZZZZZZ 8, 219–224 (2001). - PubMed
    1. Suryanarayanan S. et al. , “Comparison of tomosynthesis methods used with digital mammography,” Acad. Radiol. ZZZZZZ 7, 1085–1097 (2000). - PubMed
    1. Wu T. et al. , “Tomographic mammography using a limited number of low-dose cone-beam projection images,” Med. Phys. MPHYA610.1118/1.1543934 30, 365–380 (2003). - DOI - PubMed
    1. Niklason L. T. et al. , “Digital tomosynthesis in breast imaging,” Radiology RADLAX 205, 399–406 (1997). - PubMed

Publication types