Model for the detection of signals in images with multiple suspicious locations

Abstract

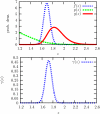
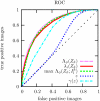
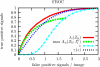
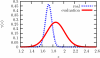
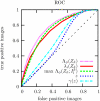
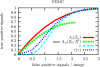
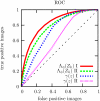
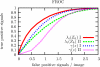
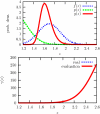
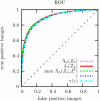
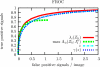
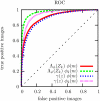
A signal detection model is presented that combines a signal model and a noise model providing mathematical descriptions of the frequency of appearance of the signals, and of the signal-like features naturally occurring in the background. We derive expressions for the likelihood functions for the whole ensemble of observed suspicious locations, in various possible combinations of signals and false signal candidates. As a result, this formalism is able to describe several new types of detection tests using likelihood ratio statistics. We have a global image abnormality test and an individual signal detection test. The model also provides an alternative mechanism in which is selected the combination of signal and noise features candidates that has the maximum likelihood. These tests can be analyzed with a variety of operating characteristic curves (ROC, LROC, FROC, etc.). In the mathematical formalism of the model, all the details characterizing the suspicious features are reduced to a single scalar function, which we name the signal specificity function, representing the frequency that a signal takes a certain value relative to the frequency of having a false signal with the same value in an image of given size. The signal specificity function ranks the degree of suspiciousness of the features found, and can be used to unify into a single score all the suspicious feature characteristics, and then apply the usual decision conventions as in the Swensson's detection model [Med. Phys. 23, 1709-1725 (1996)]. We present several examples in which these tests are compared. We also show how the signal specificity function can be used to model various degrees of accuracy of the observer's knowledge about image noise and signal statistical properties. Aspects concerning modeling of the human observer are also discussed.

Figure 1

The signal distribution f(z), the noise nodule distribution p(z), and the distribution of the maximum noise nodule distribution g(z) used in Example I (top). In the bottom graphic is plotted the signal specificity function γ(z).

Figure 2

Comparison of the ROC curves obtained for Example I by five different methods of assigning the image global abnormality score. The first method is based on the likelihood ratio statistic Λ_ϕ(Z_k), given by Eq. 19. The second method uses the maximum individual likelihood ratio λ_i(Z_k) as discussed in Sec. 2D2. The third method uses the value ${\Lambda }_{\varphi }(Z_k;I_l^k)$ of the most likely signal and noise nodule combination, as discussed in Sec. 2D3. The fourth method uses the maximum contrast z value found, and the fifth method uses the maximum signal specificity score found γ(z).

Figure 3

Comparison of the FROC curves obtained with four different methods for Example I. In the first method, the λ_i(Z_k) statistic is used, as discussed in Sec. 2D2. In the second method, also the λ_i(Z_k) statistic is used, but limited to the set of features $I_l^k$ of the most likely signal and noise nodule combination $\left[\max {\Lambda }_{\varphi }(Z_k;I_l^k)\right]$, as discussed in Sec. 2D3. The third method uses the contrast z values, and the fourth method uses the signal specificity score γ(z).

Figure 4

Comparison between the real signal specificity function and the specificity function used for image evaluation in Example II.

Figure 5

Comparison of the ROC curves for Example II. The significance of the curves is the same as in Fig. 2.

Figure 6

Comparison of the FROC curves for Example II. The significance of the curves is the same as in Fig. 3.

Figure 7

Comparisons between the ROC curves in Examples I and II for the tests using the global likelihood ratio statistic Λ_ϕ(Z_k) and the maximum specificity score γ(z).

Figure 8

Comparisons between the FROC curves in Examples I and II for the free response tests using the likelihood ratio statistic for individual suspicious locations λ_i(Z_k) and for the test using the specificity score γ(z).

Figure 9

Signal distribution f(z), noise nodule distribution p(z), and distribution of the maximum noise nodule distribution g(z) used in Example III (top). In the bottom graph, the signal specificity function γ(z) is plotted.

Figure 10

Comparison of the ROC curves for Example III. The significance of the curves is the same as in Fig. 2.

Figure 11

Comparison of the FROC curves for Example III. The significance of the curves is the same as in Fig. 3.

Figure 12

Comparison of the ROC curves obtained in Example III with the results obtained for a modified distribution of the number of signals per signal-present image ϕ₂(m), in which almost all signal-present images contain three signals.

Figure 13

Comparison of the FROC curves obtained in Example III with the results obtained for a modified distribution of the number of signals per signal-present image ϕ₂(m), in which almost all signal-present images contain three signals.