Optimizing the automatic selection of spike detection thresholds using a multiple of the noise level
- PMID: 19205769
- PMCID: PMC2734874
- DOI: 10.1007/s11517-009-0451-2
Optimizing the automatic selection of spike detection thresholds using a multiple of the noise level
Abstract
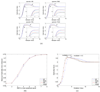
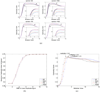
Thresholding is an often-used method of spike detection for implantable neural signal processors due to its computational simplicity. A means for automatically selecting the threshold is desirable, especially for high channel count data acquisition systems. Estimating the noise level and setting the threshold to a multiple of this level is a computationally simple means of automatically selecting a threshold. We present an analysis of this method as it is commonly applied to neural waveforms. Four different operators were used to estimate the noise level in neural waveforms and set thresholds for spike detection. An optimal multiplier was identified for each noise measure using a metric appropriate for a brain-machine interface application. The commonly used root-mean-square operator was found to be least advantageous for setting the threshold. Investigators using this form of automatic threshold selection or developing new unsupervised methods can benefit from the optimization framework presented here.
Figures


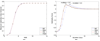

References
-
- Aksenova TI, Chibirova OK, Dryga OA, Tetko IV, Benabid AL, Villa AEP. An unsupervised automatic method for sorting neuronal spike waveforms in awake and freely moving animals. Methods. 2003;30(2):178–187. - PubMed
-
- Bankman IN, Johnson KO, Schneider W. Optimal detection, classification, and superposition resolution in neural waveform recordings. IEEE Trans Biomed Eng. 1993;40(8):836–841. - PubMed
-
- Bar-Hillel A, Spiro A, Stark E. Spike sorting: bayesian clustering of non-stationary data. J Neurosci Methods. 2006;157(2):303–316. - PubMed
-
- Benitez R, Nenadic Z. Robust unsupervised detection of action potentials with probabilistic models. IEEE Trans Biomed Eng. 2008;55(4):1344–1354. - PubMed
-
- Borghi T, Gusmeroli R, Spinelli AS, Baranauskas G. A simple method for efficient spike detection in multiunit recordings. J Neurosci Methods. 2007;163(1):176–180. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

