Breakpoint graphs and ancestral genome reconstructions
- PMID: 19218533
- PMCID: PMC2675983
- DOI: 10.1101/gr.082784.108
Breakpoint graphs and ancestral genome reconstructions
Abstract
Recently completed whole-genome sequencing projects marked the transition from gene-based phylogenetic studies to phylogenomics analysis of entire genomes. We developed an algorithm MGRA for reconstructing ancestral genomes and used it to study the rearrangement history of seven mammalian genomes: human, chimpanzee, macaque, mouse, rat, dog, and opossum. MGRA relies on the notion of the multiple breakpoint graphs to overcome some limitations of the existing approaches to ancestral genome reconstructions. MGRA also generates the rearrangement-based characters guiding the phylogenetic tree reconstruction when the phylogeny is unknown.
Figures
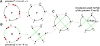
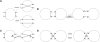

 (X, X, Q1, Q1)
(X, X, Q1, Q1)  (Q3, Q3, Q1, Q1)
(Q3, Q3, Q1, Q1)  (Q3, Q3, Q2, Q2)
(Q3, Q3, Q2, Q2)  (Q3, Q3, P3, Q2)
(Q3, Q3, P3, Q2)  (Q3, Q3, P3, P4)
(Q3, Q3, P3, P4)  (P1, Q3, P3, P4)
(P1, Q3, P3, P4)  (P1, P2, P3, P4), where r1 is a reversal in two copies of X; r2 is a fission in two copies of X; r3 is a reversal in both copies of Q1; r4 is a fission in one copy of Q2; r5 is a reversal in the other copy of Q2; r6 is a reversal in one copy of Q3; and r7 is a translocation in the other copy of Q3.
(P1, P2, P3, P4), where r1 is a reversal in two copies of X; r2 is a fission in two copies of X; r3 is a reversal in both copies of Q1; r4 is a fission in one copy of Q2; r5 is a reversal in the other copy of Q2; r6 is a reversal in one copy of Q3; and r7 is a translocation in the other copy of Q3.
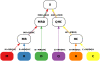
 -consistent multi-color from each pair also labels the starting node of the corresponding directed branch. Note that the tree orientation may not necessarily correlate with the time scale, and the root genome X may not necessarily be a common ancestor of the leaf genomes.
-consistent multi-color from each pair also labels the starting node of the corresponding directed branch. Note that the tree orientation may not necessarily correlate with the time scale, and the root genome X may not necessarily be a common ancestor of the leaf genomes.
 -consistent red–blue multi-color. (A) A good path on vertices x1, x2,…, x6 is transformed into a cycle on the same vertices by extending it into x0, x1, x2,…, x6, x7 and performing a 2-break on the multi-edges (x0, x1) and (x6, x7). (B) Transformation of a good cycle on 6 vertices into complete multi-edges with a 2-break on the multi-edges (x1, x2), (x3, x4) followed by a 2-break on the multi-edges (x1, x4), (x5, x6). (C) A 2-break on an irregular edge corresponds to a reversal involving chromosome ends. (D) A 2-break on two irregular edges corresponds to a fusion. (Bottom panel) Two ways of transforming a fair edge (x, y) into a good edge: (top) by a 2-break on yellow edges or (bottom) by a 2-break on green edges. In either case, the follow-up processing of the generated simple path results in the same graph with the complete multi-edge (x, y).
-consistent red–blue multi-color. (A) A good path on vertices x1, x2,…, x6 is transformed into a cycle on the same vertices by extending it into x0, x1, x2,…, x6, x7 and performing a 2-break on the multi-edges (x0, x1) and (x6, x7). (B) Transformation of a good cycle on 6 vertices into complete multi-edges with a 2-break on the multi-edges (x1, x2), (x3, x4) followed by a 2-break on the multi-edges (x1, x4), (x5, x6). (C) A 2-break on an irregular edge corresponds to a reversal involving chromosome ends. (D) A 2-break on two irregular edges corresponds to a fusion. (Bottom panel) Two ways of transforming a fair edge (x, y) into a good edge: (top) by a 2-break on yellow edges or (bottom) by a 2-break on green edges. In either case, the follow-up processing of the generated simple path results in the same graph with the complete multi-edge (x, y).


References
-
- Alekseyev M.A. Multi-break rearrangements and breakpoint re-uses: From circular to linear genomes. J. Comput. Biol. 2008;15:1117–1131. - PubMed
-
- Alekseyev M.A., Pevzner P.A. Whole genome duplications, multi-break rearrangements, and genome halving theorem. Proceedings of the 18th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA); SIAM, Philadelphia. 2007. pp. 665–679.
-
- Alekseyev M.A., Pevzner P.A. Multi-break rearrangements and chromosomal evolution. Theor. Comput. Sci. 2008;395:193–202.
-
- Amrine-Madsen H., Koepfli K.-P., Wayne R.K., Springer M.S. A new phylogenetic marker, apolipoprotein B, provides compelling evidence for eutherian relationships. Mol. Phylogenet. Evol. 2003;28:225–240. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
