Reducing the sensitivity of IMPT treatment plans to setup errors and range uncertainties via probabilistic treatment planning
- PMID: 19235384
- PMCID: PMC2673668
- DOI: 10.1118/1.3021139
Reducing the sensitivity of IMPT treatment plans to setup errors and range uncertainties via probabilistic treatment planning
Abstract
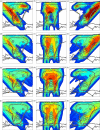
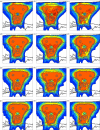
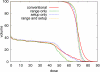
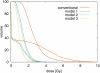
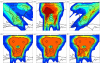
Treatment plans optimized for intensity modulated proton therapy (IMPT) may be very sensitive to setup errors and range uncertainties. If these errors are not accounted for during treatment planning, the dose distribution realized in the patient may by strongly degraded compared to the planned dose distribution. The authors implemented the probabilistic approach to incorporate uncertainties directly into the optimization of an intensity modulated treatment plan. Following this approach, the dose distribution depends on a set of random variables which parameterize the uncertainty, as does the objective function used to optimize the treatment plan. The authors optimize the expected value of the objective function. They investigate IMPT treatment planning regarding range uncertainties and setup errors. They demonstrate that incorporating these uncertainties into the optimization yields qualitatively different treatment plans compared to conventional plans which do not account for uncertainty. The sensitivity of an IMPT plan depends on the dose contributions of individual beam directions. Roughly speaking, steep dose gradients in beam direction make treatment plans sensitive to range errors. Steep lateral dose gradients make plans sensitive to setup errors. More robust treatment plans are obtained by redistributing dose among different beam directions. This can be achieved by the probabilistic approach. In contrast, the safety margin approach as widely applied in photon therapy fails in IMPT and is neither suitable for handling range variations nor setup errors.
Figures








References
-
- Flampouri S., Slopsema R., Yeung D., Malyapa R., Keole S., Vargas C., and Li Z., “Realistic estimation of proton range uncertainties and dosimetric implications,” Med. Phys. MPHYA6 34(6), 2643 (2007) (abstract).
-
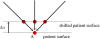
- Jäkel O. and Reiss P., “The influence of metal artefacts on the range of ion beams,” Phys. Med. Biol. PHMBA7 52(3), 653–644 (2007). - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

