The outbreak of cooperation among success-driven individuals under noisy conditions
- PMID: 19237576
- PMCID: PMC2646628
- DOI: 10.1073/pnas.0811503106
The outbreak of cooperation among success-driven individuals under noisy conditions
Abstract
According to Thomas Hobbes' Leviathan [1651; 2008 (Touchstone, New York), English Ed], "the life of man [is] solitary, poor, nasty, brutish, and short," and it would need powerful social institutions to establish social order. In reality, however, social cooperation can also arise spontaneously, based on local interactions rather than centralized control. The self-organization of cooperative behavior is particularly puzzling for social dilemmas related to sharing natural resources or creating common goods. Such situations are often described by the prisoner's dilemma. Here, we report the sudden outbreak of predominant cooperation in a noisy world dominated by selfishness and defection, when individuals imitate superior strategies and show success-driven migration. In our model, individuals are unrelated, and do not inherit behavioral traits. They defect or cooperate selfishly when the opportunity arises, and they do not know how often they will interact or have interacted with someone else. Moreover, our individuals have no reputation mechanism to form friendship networks, nor do they have the option of voluntary interaction or costly punishment. Therefore, the outbreak of prevailing cooperation, when directed motion is integrated in a game-theoretical model, is remarkable, particularly when random strategy mutations and random relocations challenge the formation and survival of cooperative clusters. Our results suggest that mobility is significant for the evolution of social order, and essential for its stabilization and maintenance.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
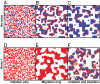

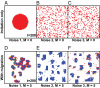


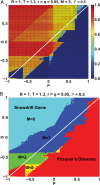
References
-
- Gonzáles MC, Hidalgo CA, Barabási AL. Understanding individual human mobility patterns. Nature. 2008;453:779–782. - PubMed
-
- Hufnagel L, Brockmann D, Geisel T. The scaling laws of human travel. Nature. 2006;439:462–465. - PubMed
-
- Batty M. Cities and Complexity. Cambridge, MA: MIT Press; 2005.
-
- Weidlich W. Sociodynamics. A Systematic Approach to Mathematical Modelling in the Social Sciences. Amsterdam, The Netherlands: Harwood Academic; 2000.
-
- Pumain D, editor. Spatial Analysis and Population Dynamics. Montrouge, France: John Libbey Eurotext; 1991.
MeSH terms
LinkOut - more resources
Full Text Sources

