Nonlinear elasticity of stiff filament networks: strain stiffening, negative normal stress, and filament alignment in fibrin gels

Abstract

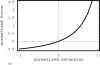
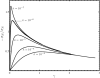
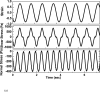
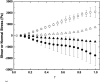
Many biomaterials formed by cross-linked semiflexible or rigid filaments exhibit nonlinear theology in the form of strain-stiffening and negative normal stress when samples are deformed in simple shear geometry. Two different classes of theoretical models have been developed to explain this nonlinear elastic response, which is neither predicted by rubber elasticity theory nor observed in elastomers or gels formed by flexible polymers. One model considers the response of isotropic networks of semiflexible polymers that have nonlinear force-elongation relations arising from their thermal fluctuations. The other considers networks of rigid filaments with linear force-elongation relations in which nonlinearity arises from nonaffine deformation and a shift from filament bending to stretching at increasing strains. Fibrin gels are a good experimental system to test these theories because the fibrin monomer assembles under different conditions to form either thermally fluctuating protofibrils with persistence length on the order of the network mesh size, or thicker rigid fibers. Comparison of rheologic and optical measurements shows that strain stiffening and negative normal stress appear at smaller strains than those at which filament orientation is evident from birefringence. Comparisons of shear to normal stresses and the strain-dependence of shear moduli and birefringence suggest methods to evaluate the applicability of different theories of rod-like polymer networks. The strain-dependence of the ratio of normal stress to shear stress is one parameter that distinguishes semiflexible and rigid filament models, and comparisons with experiments reveal conditions under which specific theories may be applicable.

Figure 1. Schematic diagram for two different mechanisms of strain stiffening

(a) Semiflexible polymers linked at ends in network junctions lose configurational entropy as their end-to-end distances increase or decrease from their resting lengths during shear deformation. Filaments with intrinsically non-linear force elongation relations resist elongation more strongly the more they are stretched to the limit at which the end-to-end distance equals their contour length. Adapted from Ref. . (b) Stiff filaments deform initially by bending at small strains and then by stretching at larger strains when their end-to-end vectors align in the shear field. In this mode, fibers with linear force-extension relations can also produce strain stiffening in networks because of the geometrical changes as they align in shear. Adapted from Ref.

Figure 2

(a) Normalized force-extension relation for a thermally fluctuating semi-flexible filament of length L derived from the model of ^, . Here, the force is in units of κπ² / L², and the strain is plotted as a multiple of $L∕{\pi }^2{\ell }_p$. (b) The ratio of normal stress to shear stress as a function of shear strain (in arbitrary units) for isotropic crosslinked networks of filaments with the force-extension relation shown in Figure 2 (a).

Figure 2

(a) Normalized force-extension relation for a thermally fluctuating semi-flexible filament of length L derived from the model of ^, . Here, the force is in units of κπ² / L², and the strain is plotted as a multiple of $L∕{\pi }^2{\ell }_p$. (b) The ratio of normal stress to shear stress as a function of shear strain (in arbitrary units) for isotropic crosslinked networks of filaments with the force-extension relation shown in Figure 2 (a).

Figure 3

The ratio of normal to shear stress versus applied strain γ for constant density $\mathrm{L}∕{\ell }_{\mathrm{c}}=15$ and various filament bending stiffnesses. Here, the bending modulus κ is normalized by μL², where μ is the stretch modulus of a filament. On decreasing filament bending stiffness (κ) a peak grows, becoming more pronounced and moving to smaller strain. For large strain the curves depend weakly on κ, showing a regime dominated by stretching only. This can explain the slowly decreasing ratio at high strain, since filament alignment with the shear direction results in a reduced fraction of stress in the normal direction.

Figure 4

(a) The raw waveforms of strain (top) and shear stress (middle) and normal stress (bottom) from the analog output of the Rheometrics RFS III instrument. The oscillatory strain (80 %) was applied to the fibrin gel at f = 1 Hz. The frequency doubling observed in the normal stress signal can be attributed to the fact that the normal stress does not depend on the shear directions. Sample condition: 2.5 mg/ml salmon fibrin gel at pH 7.4, and [NaCl] = 0.15 mM (b) The total shear stress (dark line) obtained from the raw data averaged over eight oscillatory cycles and the elastic component of shear stress (red solid single line) computed from large amplitude oscillatory shear (LAOS) analysis as functions of the oscillatory strain. (Inset) The shear modulus reported by rheometer software as a function of shear strain amplitude is plotted.

Figure 4

(a) The raw waveforms of strain (top) and shear stress (middle) and normal stress (bottom) from the analog output of the Rheometrics RFS III instrument. The oscillatory strain (80 %) was applied to the fibrin gel at f = 1 Hz. The frequency doubling observed in the normal stress signal can be attributed to the fact that the normal stress does not depend on the shear directions. Sample condition: 2.5 mg/ml salmon fibrin gel at pH 7.4, and [NaCl] = 0.15 mM (b) The total shear stress (dark line) obtained from the raw data averaged over eight oscillatory cycles and the elastic component of shear stress (red solid single line) computed from large amplitude oscillatory shear (LAOS) analysis as functions of the oscillatory strain. (Inset) The shear modulus reported by rheometer software as a function of shear strain amplitude is plotted.

Figure 5

(a) The both shear and negative normal stress are plotted versus constantly increasing strain (d γ/d t = 0.01 s^-1) for 2.5 mg/ml fibrin gels at pH 7.4 (open and solid circles) and pH 8.5 (open and solid triangles). The error bars for values at pH 7.4 were obtained by averaging three different samples. (b) The ratio of the negative normal stress to the shear stress of fibrin gels is plotted against varying strains; 4.0 mg/ml salmon fibrin at pH 8.5 (open triangles), 4.0 mg/ml salmon fibrin at pH 7.5 (solid rectangles), and 6.0 mg/ml human fibrin at pH 7.5 (solid circles). Networks of more flexible protofibrils (pH 8.5) show a more prominent overshoot in comparison with coarse networks (pH 7.5) of stiffer filaments.

Figure 5

(a) The both shear and negative normal stress are plotted versus constantly increasing strain (d γ/d t = 0.01 s^-1) for 2.5 mg/ml fibrin gels at pH 7.4 (open and solid circles) and pH 8.5 (open and solid triangles). The error bars for values at pH 7.4 were obtained by averaging three different samples. (b) The ratio of the negative normal stress to the shear stress of fibrin gels is plotted against varying strains; 4.0 mg/ml salmon fibrin at pH 8.5 (open triangles), 4.0 mg/ml salmon fibrin at pH 7.5 (solid rectangles), and 6.0 mg/ml human fibrin at pH 7.5 (solid circles). Networks of more flexible protofibrils (pH 8.5) show a more prominent overshoot in comparison with coarse networks (pH 7.5) of stiffer filaments.

Figure 6

Comparison of filament alignment with strain-stiffening. The average optical retardance (circles) increases with increased shear strain, but lags behind the increase in shear modulus (triangles) of the same sample. Sample preparation: human fibrin 3 mg/ml at pH 7.4. Above the plot are representative images takes at strain = 0, 0.3, 0.6, and 1.0 (left to right), showing increasing retardance magnitude (lightness) and correlated direction of polarization. The red lines indicate local slow axis orientations, which are increasingly aligned along the direction of applied shear strain. The scale bar represents 50 μm.