Quasispecies theory for horizontal gene transfer and recombination

Abstract

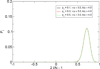
We introduce a generalization of the parallel, or Crow-Kimura, and Eigen models of molecular evolution to represent the exchange of genetic information between individuals in a population. We study the effect of different schemes of genetic recombination on the steady-state mean fitness and distribution of individuals in the population, through an analytic field theoretic mapping. We investigate both horizontal gene transfer from a population and recombination between pairs of individuals. Somewhat surprisingly, these nonlinear generalizations of quasispecies theory to modern biology are analytically solvable. For two-parent recombination, we find two selected phases, one of which is spectrally rigid. We present exact analytical formulas for the equilibrium mean fitness of the population, in terms of a maximum principle, which are generally applicable to any permutation invariant replication rate function. For smooth fitness landscapes, we show that when positive epistatic interactions are present, recombination or horizontal gene transfer introduces a mild load against selection. Conversely, if the fitness landscape exhibits negative epistasis, horizontal gene transfer or recombination introduces an advantage by enhancing selection towards the fittest genotypes. These results prove that the mutational deterministic hypothesis holds for quasispecies models. For the discontinuous single sharp peak fitness landscape, we show that horizontal gene transfer has no effect on the fitness, while recombination decreases the fitness, for both the parallel and the Eigen models. We present numerical and analytical results as well as phase diagrams for the different cases.

FIG. 1

Convention for the sign of epistasis, ε. In the figure are represented two smooth fitness landscapes, as a function of u = 2l/N − 1, with N the total length of the (binary) genetic sequences and 0 ≤ l ≤ N the number of beneficial mutations (number of ’+’ spins) along the sequence. In this representation, positive (synergistic) epistasis ε > 0 corresponds to a positive curvature f″ (u) > 0, while negative (antagonistic) epistasis ε < 0 corresponds to a negative curvarture f″ (u) < 0 [7, 11, 12]. The examples shown are a quadratic fitness landscape f(u) = ku²/2 (dashed line), with positive curvature and ε > 0, and a square-root fitness landscape $f(u)=k\sqrt{u}$ (solid line), with negative curvature and ε < 0. We set k = 4.0 in both examples.

FIG. 2

Pictorial representation of the horizontal gene transfer process considered.

FIG. 3

Phase diagram of the parallel (Kimura) model for the quadratic fitness f(u) = ku²/2, with horizontal gene transfer of non-overlapping blocks of size M̄. The phase boundary of the error threshold phase transition is given by the curve, and its shape is independent of the block size M̄. In the absence of horizontal gene transfer, the phase transition occurs at k/μ = 1.

FIG. 4

Pictorial representation of the two-parent genetic recombination process considered in the theory.

FIG. 5

Convergence of the numerical results towards the theoretical value for two-parent recombination in the parallel (Kimura) model for the sharp peak fitness. In this example, A/μ = 4.0.

FIG. 6

Probability distributions for two-parent recombination in the parallel model for the quadratic fitness f(u) = ku²/2, with k/μ = 4.0 and ν/μ = 3.0, obtained from stochastic simulations with M = 10 000 sequences of N = 100 bases and different values of p_c.

FIG. 7

Convergence of the numerical results towards the theoretical value for two-parent recombination in the parallel model for the selective phase S1 in Eq. (71). In this example, k/μ = 4.0 and ν/μ < 1/8.

FIG. 8

Convergence of the numerical results towards the theoretical value for two-parent recombination in the parallel model for the selective phase S2 in Eq. (71). In this example, k/μ = 4.0 and ν/μ > 1/8.