Noise shaping in neural populations
- PMID: 19257076
- PMCID: PMC4529323
- DOI: 10.1103/PhysRevE.79.011914
Noise shaping in neural populations
Abstract
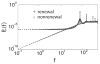
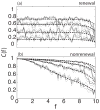
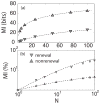
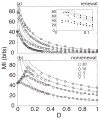
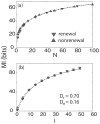
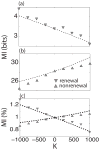
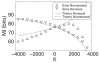
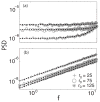
Many neurons display intrinsic interspike interval correlations in their spike trains. However, the effects of such correlations on information transmission in neural populations are not well understood. We quantified signal processing using linear response theory supported by numerical simulations in networks composed of two different models: One model generates a renewal process where interspike intervals are not correlated while the other generates a nonrenewal process where subsequent interspike intervals are negatively correlated. Our results show that the fractional rate of increase in information rate as a function of network size and stimulus intensity is lower for the nonrenewal model than for the renewal one. We show that this is mostly due to the lower amount of effective noise in the nonrenewal model. We also show the surprising result that coupling has opposite effects in renewal and nonrenewal networks: Excitatory (inhibitory coupling) will decrease (increase) the information rate in renewal networks while inhibitory (excitatory coupling) will decrease (increase) the information rate in nonrenewal networks. We discuss these results and their applicability to other classes of excitable systems.
Figures
References
-
- Yacomotti AM, Eguia MC, Aliaga J, Martinez OE, Mindlin GB, Lipsich A. Phys Rev Lett. 1999;83:292.
- Wiesenfeld K, Satija I. Phys Rev B. 1987;36:2483. - PubMed
-
- Mainen ZF, Sejnowski TJ. Science. 1995;2681503 - PubMed
-
- Bulsara A, et al. J Stat Phys. 1993;70(1)
- Gammaitoni L, et al. Rev Mod Phys. 1998;70:223.
- Moss F, Ward L, Sannita W. Clin Neurophysiol. 2004;115:267. - PubMed
-
- Izhikevich EM. Int J Bifurcation Chaos Appl Sci Eng. 2000;10:1171.
- Sherman SM. Trends Neurosci. 2001;24:122. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
