Inherent noise can facilitate coherence in collective swarm motion

Abstract

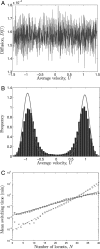
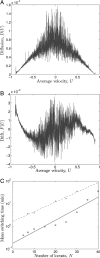
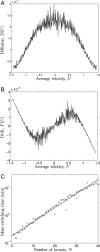
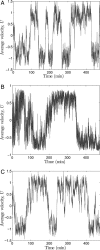
Among the most striking aspects of the movement of many animal groups are their sudden coherent changes in direction. Recent observations of locusts and starlings have shown that this directional switching is an intrinsic property of their motion. Similar direction switches are seen in self-propelled particle and other models of group motion. Comprehending the factors that determine such switches is key to understanding the movement of these groups. Here, we adopt a coarse-grained approach to the study of directional switching in a self-propelled particle model assuming an underlying one-dimensional Fokker-Planck equation for the mean velocity of the particles. We continue with this assumption in analyzing experimental data on locusts and use a similar systematic Fokker-Planck equation coefficient estimation approach to extract the relevant information for the assumed Fokker-Planck equation underlying that experimental data. In the experiment itself the motion of groups of 5 to 100 locust nymphs was investigated in a homogeneous laboratory environment, helping us to establish the intrinsic dynamics of locust marching bands. We determine the mean time between direction switches as a function of group density for the experimental data and the self-propelled particle model. This systematic approach allows us to identify key differences between the experimental data and the model, revealing that individual locusts appear to increase the randomness of their movements in response to a loss of alignment by the group. We give a quantitative description of how locusts use noise to maintain swarm alignment. We discuss further how properties of individual animal behavior, inferred by using the Fokker-Planck equation coefficient estimation approach, can be implemented in the self-propelled particle model to replicate qualitatively the group level dynamics seen in the experimental data.

Fig. 1.

Equation-free analysis of the local interaction model. L = 90, R = 5, β = 1, ω = 2.6 and N = 30 (A and B, only). (A) Estimation of the diffusion coefficient of the unavailable FPE for the coarse variable, U. (B) Two approximations of the SPD. The histogram represents a sample of the alignments (taken every 50 time steps) from one long simulation. The curve represents the equation-free estimation to the SPD. (C) Mean switching time as a function of the number of locusts, N, derived by using the equation-free technique (crosses with dashed best fit line) and from simulation (squares with full best fit line).

Fig. 2.

Analysis of the experimental data. N = 30 (A and B, only). The diffusion coefficient (A) and drift coefficient (B) estimated by using Eq. 13 with δt = 4 s, and Eq. 14 with δt = 0.2 s, respectively. The rationale behind these choices of δt is explained in SI Appendix. (C) Variation of the mean switching time with the number of locusts, calculated by using the estimated potentials and Eq. 16 (crosses with dashed best fit line) and by counting the number of direction switches (squares with full best fit line). Note the log scale on the y axis.

Fig. 3.

Analysis of the revised model. L = 90, R = 5, β = 1, ω = 2.6, |${\bar{u}}_i^{\text{loc}}$|_max> = 1.5 and N = 30 (A and B, only). The interaction radius was chosen to be consistent with ref. and the noise was chosen so as to mimic the relationship between locust number and mean switching time given by the experimental data. (A) The diffusion coefficient of the revised model mimics the quadratic shape of the actual diffusion coefficient for the locusts, peaking at approximately zero alignment. (B) The potential has two deep wells giving further favorable comparison with the experimental data. (C) Comparison of the exponential relationship between the number of locusts and mean switching time, given by the revised model (squares with full best fit line) and the experimental data (crosses with dashed best fit line). Note the log scale on the y axis.

Fig. 4.

Typical evolution of the average velocity, U, for the original model (A), the actual locust data (B), and the revised model (C). N = 30, L = 90, R = 5, β = 1,ω = 3.9 (Aand C, only) and |${\bar{u}}_i^{\text{loc}}$|_max = 1.5 (C, only). In A and C, we have used an altered value of ω and a rescaled time axis to better illustrate the similarities and differences between the models and the experimental data.