An agglomerative hierarchical approach to visualization in Bayesian clustering problems

Abstract

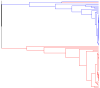
Clustering problems (including the clustering of individuals into outcrossing populations, hybrid generations, full-sib families and selfing lines) have recently received much attention in population genetics. In these clustering problems, the parameter of interest is a partition of the set of sampled individuals--the sample partition. In a fully Bayesian approach to clustering problems of this type, our knowledge about the sample partition is represented by a probability distribution on the space of possible sample partitions. As the number of possible partitions grows very rapidly with the sample size, we cannot visualize this probability distribution in its entirety, unless the sample is very small. As a solution to this visualization problem, we recommend using an agglomerative hierarchical clustering algorithm, which we call the exact linkage algorithm. This algorithm is a special case of the maximin clustering algorithm that we introduced previously. The exact linkage algorithm is now implemented in our software package PartitionView. The exact linkage algorithm takes the posterior co-assignment probabilities as input and yields as output a rooted binary tree, or more generally, a forest of such trees. Each node of this forest defines a set of individuals, and the node height is the posterior co-assignment probability of this set. This provides a useful visual representation of the uncertainty associated with the assignment of individuals to categories. It is also a useful starting point for a more detailed exploration of the posterior distribution in terms of the co-assignment probabilities.

figure 1. The exact linkage algorithm

Here we illustrate the exact linkage algorithm with an example for a sample of 5 individuals. At the initialisation step (iteration t = 0) we create 5 terminal nodes, labelled respectively 1, 2, 3, 4 and 5. This is followed by iterations t = 1, 2, 3, 4. At each iteration t (≥ 1) we begin with an update step. This is followed by an acceptance step at which we create a new internal node, labelled -t (where t is the iteration at which it is created). At the update step we update the set of proposed nodes. This updated set of proposed nodes is formed from all possible pairs of the root nodes available at the start of the present iteration. In Figure 1, every node (The height of a node is equal to the co-assignment probability of the set of individuals defined by the node) is positioned at a height equal to the co-assignment probability of the set defined by that node. The proposed nodes are arranged on the vertical axis to the right of the forest. (The height of a node is equal to the co-assignment probability of the set of individuals defined by the node.) Notice that it is always the highest proposed node which is accepted. At iteration t = 1 the proposed node (4, 5) is accepted and added to the tree, where it is labelled -1. At iteration t = 2 the proposed node (1, 2) is accepted and added to the tree, where it is labelled -2. At iteration t = 3 the proposed node (-1, 3) is accepted and added to the tree, where it is labelled -3. At iteration t = 4 the proposed node (-3, -2) is accepted and added to the tree, where it is labelled -4.

figure 2. Example 1. The true matrilineal pedigree of the simulated data set

The true matrilineal pedigree of the exhaustive sample of all n = N = 100 individuals from a single local population. Outcrossing events are indicated by diamonds. Those selfing lines which are represented in the sample by more than 2 individuals are colour-coded.

figure 3. Example 1. Output from the exact linkage algorithm

The rooted binary forest generated by applying the exact linkage algorithm to the output from the IMPPS Markov chain sampler (a pooled sample of 60 000 observations).

figure 4. Example 2. Output from the maximin agglomerative algorithm with d = 2

The rooted binary forest generated by applying the maximin agglomerative algorithm, with d = 2, to the output from the HWLER Markov chain sampler.

figure 5. Example 2. Output from the maximin agglomerative algorithm with d = 3

The rooted binary forest generated by applying the maximin agglomerative algorithm, with d = 3, to the output from the HWLER Markov chain sampler.

figure 6. Example 2. Output from the maximin agglomerative algorithm with d = 4

The rooted binary forest generated by applying the maximin agglomerative algorithm, with d = 4, to the output from the HWLER Markov chain sampler.

figure 7. Example 2. Output from the exact linkage algorithm

The rooted binary forest generated by applying the exact linkage algorithm to the output from the HWLER Markov chain sampler.