Rapid 3-D imaging of contrast flow: application in a perfused kidney phantom

Abstract

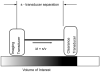
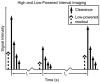
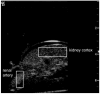
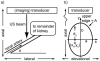
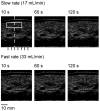
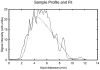
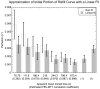
Previous studies indicate imaging of ultrasound contrast in 3-D is potentially superior to 2-D imaging for vascular characterization. A dual-beam, dynamic refill technique, which relies on volumetric contrast clearance and sequential imaging, was used to image a preserved porcine kidney perfused with contrast. A model was developed for the contrast profile across the renal artery to estimate fractional blood volume. This model was used along with refill curve information to measure absolute perfusion within renal cortex for a 100-cm(3) volume. Perfusion measurements from a slice within the volume were also made using a modified interval imaging technique. The measured perfusion using the dual-beam technique was consistent with the perfusion measured using the interval imaging technique (dual-beam values were 1.06 +/- 0.04 x corresponding interval imaging values). These experiments suggest that ultrasound contrast perfusion measurements are independent of the volume of contrast eliminated before refill.

Fig. 1

DT method schematic. As previously described (Chen et al. 2007), the DT method uses two transducers translated at a constant velocity v, with the clearance transducer translated over the tissue ahead of the imaging one. The clearance transducer clears the volume of interest and the imaging transducer reads the amount of contrast agent that has refilled since contrast clearance. Based on the separation distance s, the refill associated with a specific interval Δt can be measured. Additional delay can be added by pausing the sweep after clearance and before imaging and the two transducers can be replaced by a single volumetric imaging transducer with sufficient control for both clearance and imaging (Reprinted with permission from Chen et al. 2007).

Fig. 2

Traditional and low-power II. In a traditional II sequence, a series of high-power pulses is applied starting with the tissue being fully perfused and clearing the volume of contrast. After waiting durations I, additional clearance sequences are fired. The signal intensity from the first clearance frame of each sequence corresponds to the level of refill in interval I. Combining the refill levels after various intervals produces a refill curve. Inserting a minimally destructive low power frame immediately prior to the start of the clearance sequences allows the measurement at low power of the contrast agent signal immediately prior to each clearance sequence. These low-power data can then be directly compared to DT measurements of the same volume.

Fig. 3

Schematic of DT apparatus and experimental setup. The DT apparatus, modified from the apparatus previously reported (Chen et al. 2007), consists of a DT positioning stage driven by translation (M_T) and separation (M_S) motors. The clearance (T_c) and imaging (T_i) transducers are positioned above the phantom being scanned, with the clearance transducer positioned at the edge of the volume of interest. A pump continuously delivers dilute contrast agent from a stirred flask to the phantom.

Fig. 4

Kidney phantom with transducer orientations. The kidney phantom is perfused through the renal artery that is connected to a pump. All DT scans are acquired by translating the transducers (T_i and T_c refer to the imaging and clearance transducers, respectively) as indicated by the arrows, with the transducers oriented in the transverse orientation. II was performed in the transverse orientation for a selected slice that constitutes a portion of the scanned volume. Reconstructed images in the longitudinal direction, extracted from scans performed using the DT technique, are oriented perpendicular to the transverse orientation as shown.

Fig. 5

Example of kidney image. Depicted is a transverse image of the kidney phantom with ROIs indicated in both the cortex and renal artery. The renal artery is considered a major vessel that is always filled with contrast. From the signal profile across the vessel in the axial direction, a value A equal to the signal intensity of the contrast suspension can be derived (details in text). This value A can be used to correct for variations with the infused contrast agent suspension.

Fig. 6

Renal artery normalization model with imaging transducer directions indicated. a) The renal artery is modeled as a cylindrical tube tilted at an angle θ from the horizontal, in the same plane as the transducer. The contrast agent is intercepted by the ultrasound beam as shown. b) The intersection of the beam with the artery is an ellipse with a vessel radius a. From the geometry, the major axis b = a/cos θ. The distance d₀ from the upper-half of the curve determines the level of attenuation the agent experiences at any point (x₀, y₀) due to overlying contrast, while the unattenuated upper edge has a baseline signal level of A. The integration of the signal levels across the vessel at each depth yields the observed intensity profile (see details in the text).

Fig. 7

Computation of vessel profile. The intensity profile across the vessel is computed as follows. At every axial position y, the signal intensity P(y) is the integration of all the intensities at y with respect to the elevational direction x. These intensities are weighted by B_elevational prior to integration in order to account for the elevational beam shape. Due to the presence of attenuation from contrast agent, the intensity F(x,y) is non-uniform and is given in the text. An example of a vessel intensity profile is depicted on the right. Note how the presence of attenuation causes the peak of P(y) to shift toward the transducer from the vessel center.

Fig. 8

Representative ultrasound subtraction images obtained from a transverse slice (20 mm position) from preserved porcine kidney with low-power II and the dual-beam technique. The kidney cortex ROI is indicated by the white box. The dashed line indicates the orientation of the longitudinal slice examined with respect to the transverse slice. Note the increased echogenicity as the kidney fills with contrast over time.

Fig. 9

Representative DT longitudinal images. Analogous to the images in Fig. 8, the kidney is shown to fill with time. The reconstructed images are of lower quality than those directly obtained because the transducer point-spread function in the elevational direction is wider than in the lateral direction. In addition, the transducer spacing affects image quality in the reconstructed images. The longitudinal ROI is indicated by the white box, with the location of the 20 mm transverse slice shown by the dashed line. The locations of the other examined transverse slices from 10 to 40 mm are indicated by markers located beneath the image. Since these images are not subtraction images, the change in contrast levels is less apparent than those shown for the transverse cases in Fig. 8.

Fig. 10

Sample vessel intensity profile through renal artery. The signal intensity through the renal artery, oriented as described in the model illustrated in Fig. 6, is plotted with zero being the axial distance of the renal artery ROI closest to the transducer. The fitted curve (described in the text) is used to estimate A for the image with this profile. Note that, due to beam shape and attenuation effects, A is not the peak of the fitted curve.

Fig. 11

Fitted curves for each refill scenario (transverse slice - 20 mm position). Shown are normalized data points for each refill scenario (acquisition method, flow rate) and their fitted curve. Symbols denote individual acquisitions (each individual n) where a contrast suspension was prepared. One sees the similarity between results from the two techniques as well as the difference with the change in flow rate. The 17 mL/min cases along with the 33 mL/min II scenario were fitted with linear fits because acquired data did not extend sufficiently to permit fitting to the exponential equation. The 33 mL/min DT case depicts both its linear fit and fitted exponential.

Fig. 12

Fitted refill curves for the reconstructed longitudinal cases. Analogous to Fig. 11, the normalized data points for each flow rate are plotted with their fitted curve. Since the longitudinal images are extracted from the DT imaging, the normalization factors A_cortex used to normalize the obtained values are identical to the ones used for the DT transverse cases.

Fig. 13

Comparison of perfusion estimates for low-power II and the DT technique (20 mm position transverse slice). Slow and fast refer to the renal artery input flow rates of 17 and 33 mL/min. Error bars refer to estimated (±1 standard deviation) errors in the measurement of the parameters in question. The fast flow DT measurements were fit using both the linear and exponential models. All other measurements were fit using the linear model. The DT perfusion estimates using the linear model appear consistent (slow flow p=0.81, fast flow p=0.68) for both flow rates with those measured through II. The perfusion estimate from the exponential model fit also was not inconsistent with the II value (p=0.08).

Fig. 14

Kidney cortex perfusion values, estimated using the linear fit in order to facilitate comparisons, for selected transverse slices throughout the imaging volume. The measured perfusion at the fast rate was 5.7 ± 2.8 times that of the corresponding slow rate. The fast rate to slow rate perfusion ratio was statistically different (p=0.013) from the expected value of 2. With the possible exception of the 25 mm position, perfusion trends through the volume were consistent with the change in flow rate.

Fig. 15

Comparison of perfusion of the selected longitudinal slice at both flow rates (slow and fast being respectively 17 and 33 mL/min). The ratio of the fast rate (linear fit) to slow rate perfusion was found to be 5.7 ± 2.2, which is statistically different (p<0.05) from the expected value of 2.

Fig. 16

Approximation of the initial portion of the refill curve. Shown are the perfusion estimates found using both an exponential fit and a linear fit approximation for all fast flow cases plotted as a function of their apparent MTTs and estimated correlation coefficients between FBV and MTT from the exponential fit. The horizontal axis denotes the apparent MTT and the correlation coefficient between FBV and MTT. An exponential cannot be fit to the data as the correlation coefficient becomes 1. The horizontal axis is labeled “apparent” MTT because it is strongly suspected that the actual transit time is significantly shorter, with a corresponding reduced FBV (the 796.4 s and 873.4 s MTT cases had physically impossible values of A of 1.49 and 1.19 respectively).

Fig. 17

Effects of correlation coefficient between FBV and MTT on estimated parameters. Shown are the parameter estimates of the cases where the refill curve was estimated using the exponential expression y(t) = FBV[1-exp(-t/MTT)] plotted as a function of the estimated correlation coefficient between a) FBV and b) MTT. As the coefficient approaches 1, both the estimated parameters and their errors show large increases. c) The perfusion, r = FBV/MTT, however, does not exhibit this effect due to the effects of covariance on error estimates. d) The relative error (error of parameter/value of parameter) of the FBV and MTT also shows a large increase as the correlation coefficient approaches 1.