Internal coarse-graining of molecular systems
- PMID: 19346467
- PMCID: PMC2672529
- DOI: 10.1073/pnas.0809908106
Internal coarse-graining of molecular systems
Abstract
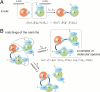
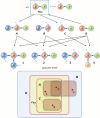
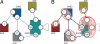
Modelers of molecular signaling networks must cope with the combinatorial explosion of protein states generated by posttranslational modifications and complex formation. Rule-based models provide a powerful alternative to approaches that require explicit enumeration of all possible molecular species of a system. Such models consist of formal rules stipulating the (partial) contexts wherein specific protein-protein interactions occur. These contexts specify molecular patterns that are usually less detailed than molecular species. Yet, the execution of rule-based dynamics requires stochastic simulation, which can be very costly. It thus appears desirable to convert a rule-based model into a reduced system of differential equations by exploiting the granularity at which rules specify interactions. We present a formal (and automated) method for constructing a coarse-grained and self-consistent dynamical system aimed at molecular patterns that are distinguishable by the dynamics of the original system as posited by the rules. The method is formally sound and never requires the execution of the rule-based model. The coarse-grained variables do not depend on the values of the rate constants appearing in the rules, and typically form a system of greatly reduced dimension that can be amenable to numerical integration and further model reduction techniques.
Conflict of interest statement
Conflict of interest statement: W.F. is a member of the Board of Directors of Plectix BioSystems Inc., a company that develops the Kappa modeling platform used in this research. J.F., V.D., J.K., and R.H. are consultants for Plectix BioSystems Inc.
Figures
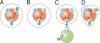
References
-
- Hlavacek WS, et al. Rules for modeling signal-transduction systems. Science STKE. 2006;344:re6. - PubMed
-
- Krüger R, Heinrich R. Model reduction and analysis of robustness for the Wnt/β-catenin signal transduction pathway. Genome Inform. 2004;15:138–148. - PubMed
-
- Faeder JR, Blinov ML, Goldstein B, Hlavacek WS. Combinatorial complexity and dynamical restriction of network flows in signal transduction. IEE Syst Biol. 2005;2:5–15. - PubMed
-
- Blinov ML, Faeder JR, Hlavacek WS. BioNetGen: Software for rule-based modeling of signal transduction based on the interactions of molecular domains. Bioinformatics. 2004;20:3289–3292. - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

