Mechanisms of receptor/coreceptor-mediated entry of enveloped viruses

Abstract

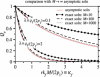
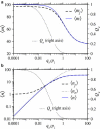
Enveloped viruses enter host cells either through endocytosis, or by direct fusion of the viral envelope and the membrane of the host cell. However, some viruses, such as HIV-1, HSV-1, and Epstein-Barr can enter a cell through either mechanism, with the choice of pathway often a function of the ambient physical chemical conditions, such as temperature and pH. We develop a stochastic model that describes the entry process at the level of binding of viral glycoprotein spikes to cell membrane receptors and coreceptors. In our model, receptors attach the cell membrane to the viral membrane, while subsequent binding of coreceptors enables fusion. The model quantifies the competition between fusion and endocytotic entry pathways. Relative probabilities for each pathway are computed numerically, as well as analytically in the high viral spike density limit. We delineate parameter regimes in which fusion or endocytosis is dominant. These parameters are related to measurable and potentially controllable quantities such as membrane bending rigidity and receptor, coreceptor, and viral spike densities. Experimental implications of our mechanistic hypotheses are proposed and discussed.

Figure 1

A schematic of the kinetic steps involved in receptor and coreceptor engagement, which ultimately lead to membrane fusion or endocytosis. Receptors and coreceptors in the cell membrane are represented by black line segments and red zigzags, respectively. The projected contact area nucleated by the number of bound receptors is also shown. Only viral spikes that have a coreceptor bound can induce fusion. Endocytosis can occur only when the contact region grows to the surface area of the virus particle. (Left) The receptors and coreceptors both bind to the same viral spikes (blue circles). An example of such a virus is HIV-1, where spikes, likely composed of trimers of gp120/41, bind to both CD4 and CCR5. (Right) An example (such as herpes simplex virus) in which coreceptors and receptors bind to different spikes, with the ratio of receptor-binding spikes (blue circles) to coreceptor-binding spikes (yellow hexagons) defined by r.

Figure 2

Two-dimensional state space for receptor and coreceptor-mediated viral entry. Each state corresponds to a virus particle bound to m ≤ M receptors and n ≤ N = rM coreceptors. In this example, the fraction of coreceptor-binding spikes to receptor-binding spikes is r = 1/2. The probability fluxes through the fusion and endocytosis pathways are indicated by the red and green arrows, respectively. A representative trajectory of the stochastic process that results in endocytosis is indicated by the blue dashed curve.

Figure 3

A schematic of a partially wrapped virus particle. The unbound spikes above the contact region are represented by light-blue circles, while the receptor-bound spikes in the contact region are represented by the dark-blue circles. Spikes that are bound to coreceptors are indicated by the red circles. The unbound receptors and coreceptors on the cell membrane (green) are not shown.

Figure 4

(a) The probability that the virus undergoes endocytosis is plotted as a function of the normalized fusion rate, k_f/p₁, for different values of the normalized coreceptor binding rate, q₁/p₁. The probability of endocytosis decreases with increasing fusion rate and, for a given fusion rate, the probability of endocytosis increases with decreasing q₁/p₁. In this example, the normalized endocytosis rate, k_e/p₁ = 1. (b) For q₁/p₁ = 1, the probability of endocytosis is plotted as a function of fusion rate for different values of the normalized endocytosis rate, k_e/p₁. In both plots, the number of receptor-binding spikes and the number of coreceptor-binding spikes are set to M = N = 100.

Figure 5

Endocytosis rates are plotted as a function of M = N. During wrapping, the fusion rate is proportional to the number of bound coreceptors, and increases with increasing N (in this case equal to M). The probability that the virus enters the cell through endocytosis decreases with increasing M = N.

Figure 6

The exact numeric solution of Eqs. 1 and 5 for the probability Q_e that the virus undergoes endocytosis is plotted as a function of κ_f ≡ rk_fM/(2p₁), the dimensionless fusion rate and compared to the M → ∞ asymptotic solution (thin solid curves). Two sets of curves, corresponding to λ ≡ q₁/(2p₁) = 0.1, 2 are shown for M = N = 10, 100, and 1000 (r = 1). In these plots, the endocytosis rate was taken to be k_e/p₁ = 2.

Figure 7

Wrapping probabilities for M = N (r = 1). (a) For q₁ ≳ p₁, the probability P_M that the virus reaches the fully wrapped state is plotted as a function of the dimensionless fusion-rate parameter rk_fM/p₁. When this parameter is small, P_M approaches unity, but when rk_fM/p₁ ≫ 1, P_M is small. (b) When 1/N ≪ q₁/p₁ ≪ 1, the wrapping probability P_M is plotted as a function of the dimensionless expression (rk_fM/p₁)(q₁/p₁). In this case, the transition of P_M from large to small values occurs at (rk_fM/p₁)(q₁/p₁) ∼ O(1). In both plots, only one parameter was varied within a group of symbols of the same color and shape. In a, the number of spikes M was varied within the groups of circles, and the fusion rate, k_f was varied within the groups of triangles. In b, the number of spikes M was varied within the groups of solid circles, the fusion rate k_f was varied within the groups of open circles, and the coreceptor binding rate q₁ was varied within the groups of triangles.

Figure 8

(a) Normalized mean times to fusion and endocytosis plotted as functions of k_f/p₁, the fusion rate per coreceptor-spike complex. Parameters used were M = N = 100, q₁/p₁ = 50, k_e/p₁ = 0.001. (b) Normalized mean times to fusion and endocytosis plotted as functions of k_e/p₁. Here, M = N = 100, q₁/p₁ = 5, and k_f/p₁ = 10⁻⁶, were used. For reference, Q_e, the corresponding probability that the virus undergoes endocytosis is also plotted.

Figure 9

(a) The mean number of receptors bound at the moment of viral fusion, and the mean number of receptors bound at the moment of viral entry (regardless of entry pathway) plotted as functions of the normalized coreceptor binding rate, q₁/p₁. (b) The mean number of coreceptors bound at the moment of fusion and endocytosis, and the average number of coreceptors bound are plotted as a function of the normalized coreceptor binding rate q₁/p₁. The probability that the virus undergoes endocytosis, Q_e is plotted for reference. For both plots M = N = 100, k_f/p₁ = 0.1, k_e/p₁ = 1.

Figure 10

Qualitative phase diagram showing the regimes of parameter space in which endocytosis is dominant. Diagrams a–c correspond to fast, intermediate, and slow coreceptor binding, respectively. In all diagrams, parameters falling within the blue region left of the vertical thick dashed line favor full viral wrapping before fusion occurs (P_M ≈ 1). In the yellow sector above the thin-dashed curves, the rate of endocytosis exceeds the effective rate of fusion in the fully wrapped state. In the green intersection of these regions, the virus is likely to reach the fully wrapped state and undergo endocytosis. Note that when coreceptor binding is very slow (c), the virus reaches the fully wrapped state for all values of k_f.