Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2009 May 29;42(8):1069-74.
doi: 10.1016/j.jbiomech.2009.02.021. Epub 2009 Apr 8.

Determinants of friction in soft elastohydrodynamic lubrication

Taraneh Moghani  1 , James P Butler, Stephen H Loring
Affiliations

Determinants of friction in soft elastohydrodynamic lubrication

Taraneh Moghani et al. J Biomech. .

Abstract

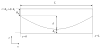
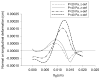
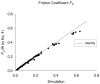
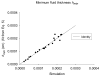
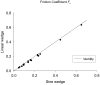
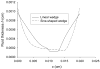
Elastohydrodynamic lubrication (EHL) protects soft tissues from damage and wear in many biological systems (e.g. synovial joints, cornea of the eye, and pleural surfaces of the lung and chest wall). Among studies of lubrication of deformable solids, few have examined the effects of external loads, geometry, and material properties on EHL of soft tissues. To examine these effects, we studied the tribology of soft tissues in a two-dimensional finite element simulation of a thin layer of fluid separating a sliding rigid surface from a soft asperity or bump with an initial sinusoidal shape. We computed the frictional force, deformation of the solid, and change in fluid thickness as functions of independent variables: sliding velocity, normal load, material properties, and bump amplitude and length. Double-logarithmic regression was used to determine the exponents of the scaling relationships of friction coefficient and minimum fluid thickness to the independent variables. The analysis showed that frictional shear force is strongly dependent on velocity, viscosity, and load, moderately dependent on bump length and elasticity, and only weakly dependent on the bump amplitude. The minimum fluid thickness is strongly dependent on velocity and viscosity, and changes moderately with load, elasticity, amplitude, and length. The shape of the bump has little effect. The results confirm that the shear-induced deformation of an initially symmetrical shape, including generalizations to other symmetrical geometries such as quadratic or piecewise linear bumps, leads to load-supporting behavior.

PubMed Disclaimer

Conflict of interest statement

Conflict of interest statement

The authors have no financial or other interest that could affect the objectivity with which they approach the subject matter of this investigation.

Figures

Figure 1
Figure 1
The undeformed geometry of solid and fluid models.
Figure 2
Figure 2
Upper panel: Pressure distribution for the deformed model under reference conditions (Table 1) with V = 0.6 cm/s. Note the asymmetry of the pressure distribution and preponderance of positive pressure under the asymmetrically deformed bump. Lower panel: Pressure distribution as above but with V = 0.02 cm/s. Fluid is thinner, and the pressure variations are more concentrated at the central, flattened region of the bump. (Pressures on the scale are in Pa × 10.)
Figure 3
Figure 3
Friction coefficient as functions of dimensionless groups.
Figure 4
Figure 4
Normal and longitudinal deformation under 2 normal pressures. Normal and longitudinal displacements are of similar magnitude.
Figure 5
Figure 5
Minimum fluid thickness as a function of dimensionless groups.
Figure 6
Figure 6
Fluid thickness as a function of position under bumps of amplitudes A = 0.0005 and A = 0.001 cm at V = 0.6 cm/s and FN = 40μN.
Figure 7
Figure 7
Friction coefficient from Eq. 4 compared to simulation data.
Figure 8
Figure 8
Minimum fluid thickness from Eq. 5 compared to simulation data.
Figure 9
Figure 9
Comparison of friction coefficients between two geometries: sine-shaped wedge and piecewise linear wedge.
Figure 10
Figure 10
Comparison of fluid thickness for sine-shaped wedge and linear wedge at V = 0.6 cm/sec, A= 0.001 cm, P = 20 Pa, E = 500 Pa, μ = 0.001 Pa·s.
See this image and copyright information in PMC

References

    1. Dowson D, Jin ZM. Micro-elastohydrodynamic lubrication of synovial joints. Engineering in Medicine. 1986;15:63–5. - PubMed
    1. Dowson D, Jin ZM. Microelastohydrodynamic lubrication of low-elastic-modulus solids on rigid substrates. Journal of Physics D: Applied Physics. 1992;25:A116–A123.
    1. Gouldstone A, Brown RE, Butler JP, Loring SH. Elastohydrodynamic separation of pleural surfaces during breathing. Respiratory Physiology & Neurobiology. 2003;137:97–106. - PubMed
    1. Hamrock BJ. Fundamentals of fluid film lubrication. McGraw-Hill; 1994. p. 42.
    1. Jin ZM, Dowson D. A general analytical solution to the problem of microelastohydrodynamic lubrication of low elastic modulus compliant bearing surfaces under line contact conditions. Proceedings of the Institution of Mechanical Engineers; 1997. pp. 265–272.

Publication types