Fermi surface nesting induced strong pairing in iron-based superconductors

Abstract

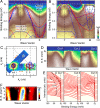
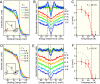
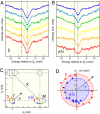
The discovery of high-temperature superconductivity in iron pnictides raised the possibility of an unconventional superconducting mechanism in multiband materials. The observation of Fermi-surface (FS)-dependent nodeless superconducting gaps suggested that inter-FS interactions may play a crucial role in superconducting pairing. In the optimally hole-doped Ba(0.6)K(0.4)Fe(2)As(2), the pairing strength is enhanced simultaneously (2Delta/T(c) approximately 7) on the nearly nested FS pockets, i.e., the inner hole-like (alpha) FS and the 2 hybridized electron-like FSs, whereas the pairing remains weak (2Delta/T(c) approximately 3.6) in the poorly nested outer hole-like (beta) FS. Here, we report that in the electron-doped BaFe(1.85)Co(0.15)As(2), the FS nesting condition switches from the alpha to the beta FS due to the opposite size changes for hole- and electron-like FSs upon electron doping. The strong pairing strength (2Delta/T(c) approximately 6) is also found to switch to the nested beta FS, indicating an intimate connection between FS nesting and superconducting pairing, and strongly supporting the inter-FS pairing mechanism in the iron-based superconductors.

Fig. 1.

Fermi surface and band structure of electron-doped BaFe_1.85Co_0.15As₂. (A and B) ARPES intensity plots of BaFe_1.85Co_0.15As₂ (T_c = 25.5 K) as a function of wave vector and binding energy measured at 8 K along the ΓX (A) and the ΓM (B) lines with the He Iα (hν = 21.218 eV) resonance line, together with the band dispersion from the first-principle calculations for k_z = 0 and π (blue and red curves, respectively). Calculated bands for BaFe₂As₂ (15) were shifted downward by 40 meV and then renormalized by the factor of 2. Green broken lines denote the expected E_F positions of BaFe₂As₂ and Ba_0.6K_0.4Fe₂As₂. (C) FS contour determined by plotting the ARPES spectral intensity integrated within ± 5meV with respect to E_F. Black filled circles show the k_F positions determined by tracing the experimental band dispersion, whereas blue open circles are symmetrized k_F points obtained by assuming a 4-fold symmetry with respect to the Γ and M point, respectively. The symmetrized k_F points (blue open circles) coincide well with the original ones (black filled circles), confirming the validity of this symmetry operation. Orange arrows show the polarization vector of the incident light for each cut. (D) ARPES spectral intensity at 8 K as a function of wave vector and binding energy. (E) Corresponding EDCs measured along 3 representative cuts 1–3 shown in C. Circles in E traces the energy dispersion of the α and β bands. (F) Second derivative plot of MDCs along cut 3 to highlight the presence of another weaker electron-like band (δ).

Fig. 2.

Temperature dependence of the superconducting gap. (A) T dependence of EDC measured at a k_F point on the β FS (red dot in Inset). (B) Symmetrized EDCs and the same but divided by the spectra at T = 33 K. Dashed line denotes the position of SC coherence peak. (C) T dependence of the SC gap size. Solid line is the BCS mean-field gap with T_c = 25.5 K and Δ(0) = 7 meV. (D–F) same as A–C but measured on the k_F point of the ellipsoidal electron pocket. Dashed line in F is the same as the solid line in C.

Fig. 3.

Momentum dependence of the superconducting gap. (A and B) Symmetrized EDCs at 8 K measured at various k_F points on the β and electron-like FS, labeled by respective colored symbols correspondingly. (C) Extracted FS from the ARPES measurements together with the definition of FS angle (θ). (D) SC gap values at 8 K as a function of θ extracted from the EDCs shown on the polar plot, for the β and electron-like FSs (red and blue dots, respectively). Dashed circles represent the averaged gap value.