The role of environmental transmission in recurrent avian influenza epidemics
- PMID: 19360126
- PMCID: PMC2660440
- DOI: 10.1371/journal.pcbi.1000346
The role of environmental transmission in recurrent avian influenza epidemics
Abstract
Avian influenza virus (AIV) persists in North American wild waterfowl, exhibiting major outbreaks every 2-4 years. Attempts to explain the patterns of periodicity and persistence using simple direct transmission models are unsuccessful. Motivated by empirical evidence, we examine the contribution of an overlooked AIV transmission mode: environmental transmission. It is known that infectious birds shed large concentrations of virions in the environment, where virions may persist for a long time. We thus propose that, in addition to direct fecal/oral transmission, birds may become infected by ingesting virions that have long persisted in the environment. We design a new host-pathogen model that combines within-season transmission dynamics, between-season migration and reproduction, and environmental variation. Analysis of the model yields three major results. First, environmental transmission provides a persistence mechanism within small communities where epidemics cannot be sustained by direct transmission only (i.e., communities smaller than the critical community size). Second, environmental transmission offers a parsimonious explanation of the 2-4 year periodicity of avian influenza epidemics. Third, very low levels of environmental transmission (i.e., few cases per year) are sufficient for avian influenza to persist in populations where it would otherwise vanish.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

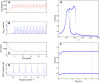
 ,
,  and
and  versus
versus  ; note the logarithmic scale for
; note the logarithmic scale for  . The initial conditions are
. The initial conditions are  ,
,  ,
,  ,
,  and
and  . The parameters are as in Table 1 with
. The parameters are as in Table 1 with  and
and  . Panel D shows the Fourier power spectrum density of
. Panel D shows the Fourier power spectrum density of  over a time interval of 25,000 years. Panels E and F
show bifurcations diagrams of the model versus
over a time interval of 25,000 years. Panels E and F
show bifurcations diagrams of the model versus  and
and  , respectively. The orbits are sampled yearly, at the
end of the wintering season. The dotted lines mark the positions of the
orbit presented on the left within the corresponding bifurcation
diagrams.
, respectively. The orbits are sampled yearly, at the
end of the wintering season. The dotted lines mark the positions of the
orbit presented on the left within the corresponding bifurcation
diagrams.
 ,
,  and
and  versus
versus  ; note the logarithmic scale for
; note the logarithmic scale for  . The initial conditions are
. The initial conditions are  ,
,  ,
,  ,
,  and
and  . The parameters are as in Table 1 with
. The parameters are as in Table 1 with  and
and  . The blue line in panel D shows the Fourier power
spectrum density of
. The blue line in panel D shows the Fourier power
spectrum density of  over a time interval of 3,500 years. The yellow line
represents the moving average of the spectrum density. Panels E and F
show the global spectral decomposition in Difference-of-Gaussians (DoG)
wavelets of stochastic orbits versus
over a time interval of 3,500 years. The yellow line
represents the moving average of the spectrum density. Panels E and F
show the global spectral decomposition in Difference-of-Gaussians (DoG)
wavelets of stochastic orbits versus  and
and  , respectively. Each spectrum is an average over 100
wavelet transforms of individual stochastic realizations of the orbit
over 3,300 years (this time interval gives 95% confidence to
the peaks of each wavelet transform; the fluctuations are due to the
stochasticity of the realizations of the model). The color map
represents the power scale measured in
, respectively. Each spectrum is an average over 100
wavelet transforms of individual stochastic realizations of the orbit
over 3,300 years (this time interval gives 95% confidence to
the peaks of each wavelet transform; the fluctuations are due to the
stochasticity of the realizations of the model). The color map
represents the power scale measured in  . The dotted lines mark the positions of the stochastic
realization presented on the left within the corresponding panels.
. The dotted lines mark the positions of the stochastic
realization presented on the left within the corresponding panels.

 and the environmental infectiousness
and the environmental infectiousness  of the time average of the A direct transmission rate;
B environmental transmission rate and the average (over stochastic
realizations) fraction of time when the C direct transmission is not
zero; D environmental transmission is not zero. The simulation details
are the same as for Figure
4.
of the time average of the A direct transmission rate;
B environmental transmission rate and the average (over stochastic
realizations) fraction of time when the C direct transmission is not
zero; D environmental transmission is not zero. The simulation details
are the same as for Figure
4.
 at environmental infectiousness
at environmental infectiousness  .
.
References
-
- Bolker B, Grenfell B. Space, persistence and dynamics of measles epidemics. Philos Trans R Soc Lond B Biol Sci. 1995;348:309–320. - PubMed
-
- Keeling MJ, Grenfell BT. Disease extinction and community size: modeling the persistence of measles. Science. 1997;275:65–67. - PubMed
-
- Bartlett MS. Measles periodicity and community size (with discussion). J R Stat Soc Ser A. 1957;120:48–70.
-
- Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proc R Soc London. 1927;115:700–721.
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

