Dissociating variability and effort as determinants of coordination
- PMID: 19360132
- PMCID: PMC2661023
- DOI: 10.1371/journal.pcbi.1000345
Dissociating variability and effort as determinants of coordination
Abstract
When coordinating movements, the nervous system often has to decide how to distribute work across a number of redundant effectors. Here, we show that humans solve this problem by trying to minimize both the variability of motor output and the effort involved. In previous studies that investigated the temporal shape of movements, these two selective pressures, despite having very different theoretical implications, could not be distinguished; because noise in the motor system increases with the motor commands, minimization of effort or variability leads to very similar predictions. When multiple effectors with different noise and effort characteristics have to be combined, however, these two cost terms can be dissociated. Here, we measure the importance of variability and effort in coordination by studying how humans share force production between two fingers. To capture variability, we identified the coefficient of variation of the index and little fingers. For effort, we used the sum of squared forces and the sum of squared forces normalized by the maximum strength of each effector. These terms were then used to predict the optimal force distribution for a task in which participants had to produce a target total force of 4-16 N, by pressing onto two isometric transducers using different combinations of fingers. By comparing the predicted distribution across fingers to the actual distribution chosen by participants, we were able to estimate the relative importance of variability and effort of 1:7, with the unnormalized effort being most important. Our results indicate that the nervous system uses multi-effector redundancy to minimize both the variability of the produced output and effort, although effort costs clearly outweighed variability costs.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
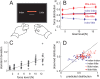
 ) depending on goal force level and finger combination, averaged over all participants. (C) Standard deviation (N) of a representative index finger of one participant as a function of the mean produced force level. The slope of the regression line corresponds to the coefficient of variation. (D) Optimal solution for force distribution across finger based on assumption that only variability was optimized (x-axis) vs. produced force distribution (y-axis).
) depending on goal force level and finger combination, averaged over all participants. (C) Standard deviation (N) of a representative index finger of one participant as a function of the mean produced force level. The slope of the regression line corresponds to the coefficient of variation. (D) Optimal solution for force distribution across finger based on assumption that only variability was optimized (x-axis) vs. produced force distribution (y-axis).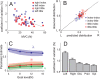
 ), normalized effort (
), normalized effort ( ), and accuracy costs (
), and accuracy costs ( ) for all force levels. (D) Coefficient of variation (CV) for left: left finger alone, right: right finger alone, obs: observed in bimanual trials, pred: calculated based on unimanual CVs for the observed combination of fingers; opt: optimal CV based on unimanual CVs and optimal combination (Eq. 1).
) for all force levels. (D) Coefficient of variation (CV) for left: left finger alone, right: right finger alone, obs: observed in bimanual trials, pred: calculated based on unimanual CVs for the observed combination of fingers; opt: optimal CV based on unimanual CVs and optimal combination (Eq. 1).References
-
- Bernstein NA. The co-ordination and regulation of movement. Oxford, UK: Pergamon; 1967.
-
- Hoffman DS, Strick PL. Step-tracking movements of the wrist. IV. Muscle activity associated with movements in different directions. J Neurophysiol. 1999;81:319–333. - PubMed
-
- Kording K. Decision theory: what “should” the nervous system do? Science. 2007;318:606–610. - PubMed
-
- Harris CM, Wolpert DM. Signal-dependent noise determines motor planning. Nature. 1998;394:780–784. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

