Flow-induced clustering and alignment of vesicles and red blood cells in microcapillaries
- PMID: 19369212
- PMCID: PMC2669370
- DOI: 10.1073/pnas.0811484106
Flow-induced clustering and alignment of vesicles and red blood cells in microcapillaries
Abstract
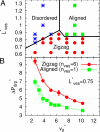
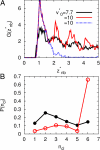
The recent development of microfluidic devices allows the investigation and manipulation of individual liquid microdroplets, capsules, and cells. The collective behavior of several red blood cells (RBCs) or microcapsules in narrow capillaries determines their flow-induced morphology, arrangement, and effective viscosity. Of fundamental interest here is the relation between the flow behavior and the elasticity and deformability of these objects, their long-range hydrodynamic interactions in microchannels, and thermal membrane undulations. We study these mechanisms in an in silico model, which combines a particle-based mesoscale simulation technique for the fluid hydrodynamics with a triangulated-membrane model. The 2 essential control parameters are the volume fraction of RBCs (the tube hematocrit, H(T)), and the flow velocity. Our simulations show that already at very low H(T), the deformability of RBCs implies a flow-induced cluster formation above a threshold flow velocity. At higher H(T) values, we predict 3 distinct phases: one consisting of disordered biconcave-disk-shaped RBCs, another with parachute-shaped RBCs aligned in a single file, and a third with slipper-shaped RBCs arranged as 2 parallel interdigitated rows. The deformation-mediated clustering and the arrangements of RBCs and microcapsules are relevant for many potential applications in physics, biology, and medicine, such as blood diagnosis and cell sorting in microfluidic devices.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
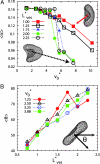
 α
α , which measures the deviation from a spherical shape, as a function of the mean flow velocity v*0. Here, the asphericity is given by α = [ (λ1 − λ2)2 + (λ2 − λ3)2 + (λ3 − λ1)2]/2Rg4, with the eigenvalues λ1 ≤ λ2 ≤ λ3 of the gyration tensor and the squared radius of gyration Rg2 = λ1 + λ2 + λ3. RBCs transits from the discocyte (with
, which measures the deviation from a spherical shape, as a function of the mean flow velocity v*0. Here, the asphericity is given by α = [ (λ1 − λ2)2 + (λ2 − λ3)2 + (λ3 − λ1)2]/2Rg4, with the eigenvalues λ1 ≤ λ2 ≤ λ3 of the gyration tensor and the squared radius of gyration Rg2 = λ1 + λ2 + λ3. RBCs transits from the discocyte (with  α
α ≃ 0.15) to the parachute shape (with
≃ 0.15) to the parachute shape (with  α
α ≲ 0.05). Simulation snapshots show the parachute (Lower Left) and bowl (Upper Right) shapes for v*0 = 7.7 with L*ves = 2.25 and L*ves = 1, respectively. (B) Average inclination angle
≲ 0.05). Simulation snapshots show the parachute (Lower Left) and bowl (Upper Right) shapes for v*0 = 7.7 with L*ves = 2.25 and L*ves = 1, respectively. (B) Average inclination angle  θ
θ for a discocyte vesicle for low flow velocities v*0 < v*c, as a function of the vesicle distance Lves. The inclination angle θ measures the deviation of the vesicle symmetry axis (determined by the eigenvector associated with the minimum eigenvalue of the gyration tensor) with the flow direction (z axis).
for a discocyte vesicle for low flow velocities v*0 < v*c, as a function of the vesicle distance Lves. The inclination angle θ measures the deviation of the vesicle symmetry axis (determined by the eigenvector associated with the minimum eigenvalue of the gyration tensor) with the flow direction (z axis).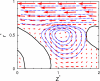


References
-
- Gompper G, Kroll DM. In: Mechanics of Membranes and Surfaces. 2nd Ed. Nelson DR, Piran T, Weinberg S, editors. Singapore: World Scientific; 2004. pp. 359–426.
-
- Seifert U. Configurations of fluid membranes and vesicles. Adv Phys. 1997;46:13–137.
-
- Vaziri A, Gopinath A. Cell and biomolecular mechanics in silico. Nat Mater. 2008;7:15–23. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

