A re-evaluation of random-effects meta-analysis
- PMID: 19381330
- PMCID: PMC2667312
- DOI: 10.1111/j.1467-985X.2008.00552.x
A re-evaluation of random-effects meta-analysis
Abstract
Meta-analysis in the presence of unexplained heterogeneity is frequently undertaken by using a random-effects model, in which the effects underlying different studies are assumed to be drawn from a normal distribution. Here we discuss the justification and interpretation of such models, by addressing in turn the aims of estimation, prediction and hypothesis testing. A particular issue that we consider is the distinction between inference on the mean of the random-effects distribution and inference on the whole distribution. We suggest that random-effects meta-analyses as currently conducted often fail to provide the key results, and we investigate the extent to which distribution-free, classical and Bayesian approaches can provide satisfactory methods. We conclude that the Bayesian approach has the advantage of naturally allowing for full uncertainty, especially for prediction. However, it is not without problems, including computational intensity and sensitivity to a priori judgements. We propose a simple prediction interval for classical meta-analysis and offer extensions to standard practice of Bayesian meta-analysis, making use of an example of studies of 'set shifting' ability in people with eating disorders.
Figures

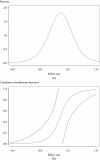
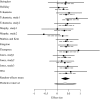
References
-
- Abrams KR, Sanso B. Approximate Bayesian inference in random effects meta-analysis. Statist. Med. 1998;17:201–218. - PubMed
-
- Ades AE, Lu G, Higgins J P T. The interpretation of random-effects meta-analysis in decision models. Med. Decsn Mak. 2005;25:646–654. - PubMed
-
- Aitkin M. A general maximum likelihood analysis of variance components in generalized linear models. Biometrics. 1999a;55:117–128. - PubMed
-
- Aitkin M. Meta-analysis by random effect modelling in generalized linear models. Statist. Med. 1999b;18:2343–2351. - PubMed
-
- Anello C, Fleiss JL. Exploratory or analytic meta-analysis: should we distinguish between them? J. Clin. Epidem. 1995;48:109–116. - PubMed
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
