A model of action potentials and fast Ca2+ dynamics in pancreatic beta-cells

Abstract

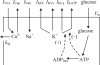
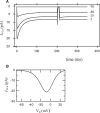
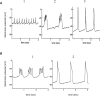
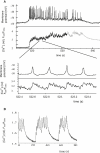
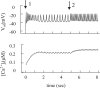
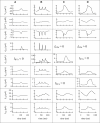
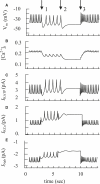
We examined the ionic mechanisms mediating depolarization-induced spike activity in pancreatic beta-cells. We formulated a Hodgkin-Huxley-type ionic model for the action potential (AP) in these cells based on voltage- and current-clamp results together with measurements of Ca(2+) dynamics in wild-type and Kv2.1 null mouse islets. The model contains an L-type Ca(2+) current, a "rapid" delayed-rectifier K(+) current, a small slowly-activated K(+) current, a Ca(2+)-activated K(+) current, an ATP-sensitive K(+) current, a plasma membrane calcium-pump current and a Na(+) background current. This model, coupled with an equation describing intracellular Ca(2+) homeostasis, replicates beta-cell AP and Ca(2+) changes during one glucose-induced spontaneous spike, the effects of blocking K(+) currents with different inhibitors, and specific complex spike in mouse islets lacking Kv2.1 channels. The currents with voltage-independent gating variables can also be responsible for burst behavior. Original features of this model include new equations for L-type Ca(2+) current, assessment of the role of rapid delayed-rectifier K(+) current, and Ca(2+)-activated K(+) currents, demonstrating the important roles of the Ca(2+)-pump and background currents in the APs and bursts. This model provides acceptable fits to voltage-clamp, AP, and Ca(2+) concentration data based on in silico analysis.

Figure 1

Schematic diagram of the ionic current and Ca²⁺ fluxes. Transmembrane currents are the I_VCa, the I_Cap, the I_Nab, the I_KDr, the I_KVs; the I_KCa; and the I_KATP. Calcium enters the β-cells primarily through voltage-activated Ca²⁺ channels by diffusion along an inwardly-directed electrochemical gradient. At the plasma membrane, two processes are involved in transporting Ca²⁺ out of the cell: a Ca²⁺ pump, and removal of Ca²⁺ sequestrated in insulin granules by exocytosis (coefficient k_sq).

Figure 2

(A) Simulation of voltage-clamp experiments for a Ca²⁺ current (I_VCa), using a double-pulse protocol. The membrane potential was stepped from the holding potential (−70 mV), where d_Ca = 0.00244 and f_2Ca = 0.884, to the prepulse potential (pointed in figure) for 200 ms. Voltage was then stepped back to the holding potential (−70 mV) for 10 ms and finally stepped to test potential. Current record simulations were made for prepulses (−70, −35, −20, −5 mV). (B) Simulated voltage dependence of whole-cell peak calcium currents obtained as in the left part of Fig. 2 A. Current parameters and equations for I_VCa are shown in Table 1 and the Appendix.

Figure 3

(A) Control islets from wild-type mouse treated with stromatoxin and TEA. Control islet electrical activity was recorded during treatment of 14 mM glucose alone (1), or in combination with 100 nM stromatoxin ScTx-1 (2) or 15 mM TEA (3). Representative APs are shown. (B) Kv2.1^−/− islet electrical activity in response to 14 mM glucose (1) or in combination with 15 mM TEA (2). Representative APs are shown.

Figure 4

Experiments with relative Ca²⁺ measurement (as F₅₃₅/F_535o (13–15)). (A) Glucose-induced bursts and spikes with simultaneous APs and Ca²⁺ measurement in control islets from wild-type mouse during treatment with 14 mM glucose. The lower record represents, at a faster timescale, part of the upper record. (B) TEA-induced bursts and Ca²⁺ spikes in control mouse islet at 14 mM glucose and 20 mM TEA.

Figure 5

Modeling of spontaneous glucose-stimulated spikes and changes of the intracellular Ca²⁺ concentration. Glucose-induced spikes were simulated at a step decrease of the free [ADP]_i at arrow 1 from a high to an intermediate value (from 100 μM to 15 μM) at t = 0 and at initial parameters as in Table 2; all other parameter settings are standard (Table 1). To simulate a glucose increase, the free [ADP]_i was decreased from 15 μM to 8 μM at arrow 2. (B) Corresponding changes in [Ca²⁺]_i were simulated using Eq. 2.

Figure 6

Simulated glucose-induced spike behavior and [Ca²⁺]_i. of glucose-induced spikes with the same initial simulation as in the beginning of Fig. 5 (A) and of Kv2.1 channel blocking (B). For simulation of Kv2.1 channel blocking, the maximal conductance (g_mKDr) for the delayed rectifier K⁺ channels was decreased from 45,000 pS to 4500 pS, and τ_dKDr was decreased from 25 ms to 20 ms. (C and D) Simulation of TEA action. In both cases, the maximal conductance for TEA-dependent K⁺ channels was decreased: from 30,000 to 15,000 pS for K_ATP (g_mATP), and from 45,000 pS to 45 pS for delayed-rectifier K⁺ channels (g_mKDr). In addition, for the mechanism in C, the maximal conductance for K_Ca channels (g_mKCa) was decreased from 20 pS to 0.1 pS. In the case of the mechanism in D, g_mKCa was increased from 20 to 200 pS and K_KCa was increased from 0.1 μM to 0.3 μM (Eq. A17). However, I_KVs was eliminated (g_mKs = 0).

Figure 7

Simulation of single spikes. Action potential (V_m), [Ca]_i, I_VCa, I_KDr, I_KVs, I_KATP I_KCa, I_Cap, and I_Nab are represented for one characteristic spike. The units are shown in series, as labeled in the first column, if no units are represented on the axis. (A) The model solution is represented for the spike after simulation of glucose addition as in Fig. 5 or Fig. 6A. The I_KVs and I_KCa currents are minor contributors in this mode of oscillation. (B) A single characteristic spike after simulation of Kv2.1 blocker application, as in Fig. 6B. The I_Cap and I_KVs currents are the major contributors in this repolarizing part of the AP. (C) A single characteristic spike after simulation of TEA action as in Fig. 6C. The proposal for full blocking of I_KCa current was accepted (I_KCa ≈ 0). The I_KVs and I_Cap currents are the major contributors in this repolarizing part of the AP. (D) A single characteristic spike as in Fig. 6D after simulation of TEA action in a model that incorporates Ca²⁺-dependent TEA-independent K⁺ channels (current I_KCa) instead of a slow-activated TEA-insensitive K⁺ current (I_KVs = 0). In this case, g_mKCa = 200 pS, K_KCa = 0.3 μM (Eq. A17) and g_mKs = 0. The I_KCa and I_Cap currents are the major contributors in the repolarizing part of AP.

Figure 8

Simulation of glucose-induced burst activity and [Ca²⁺]_i with the initial simulation, as in Fig. 6A for glucose-induced spikes in wild-type mouse. (A–C) Action potential (A), [Ca²⁺]_i (B), and I_KATP change (C) as regulators of bursting. Slow electrical bursting and [Ca²⁺]_i changes were simulated by a step increase and decrease of the K_ATP channel conductance by changes in [ADP_f]_i. At arrow 1, the [ADP_f]_i was increased from 15 μM to 20 μM, at arrow 2 from 20 μM to 25 μM, and at arrow 3 from 25 μM back to 15 μM. (D) I_KCa change as a regulator of bursting. AP and [Ca²⁺]_i oscillations were simulated at a step increase and decrease of the K_Ca channel conductance. At arrow 1, the g_mKCa was increased from 20 pS to 35 pS, at arrow 2 from 35 pS to 50 pS, and at arrow 3 from 50 pS back to 20 pS. Only I_KCa is shown. AP and [Ca²⁺]_i changes were the same as in Fig. 8, A and B. (E) I_Nab change as a regulator of bursting. AP and [Ca²⁺]_i oscillations were simulated at a step decrease and increase of the Na⁺ background current (I_Nab) conductance. At arrow 1, the g_mNab was decreased from 25 pS to 20 pS, at arrow 2 from 20 pS to 15 pS, and at arrow 3 from 15 pS back to 25 pS. Only I_Nab is shown. AP and [Ca²⁺]_i changes were the same as in Fig. 8, A and B.