The ordered extension of pseudopodia by amoeboid cells in the absence of external cues

Abstract

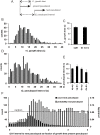
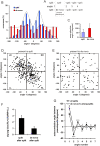
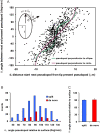
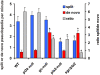
Eukaryotic cells extend pseudopodia for movement. In the absence of external cues, cells move in random directions, but with a strong element of persistence that keeps them moving in the same direction Persistence allows cells to disperse over larger areas and is instrumental to enter new environments where spatial cues can lead the cell. Here we explore cell movement by analyzing the direction, size and timing of approximately 2000 pseudopodia that are extended by Dictyostelium cells. The results show that pseudpopod are extended perpendicular to the surface curvature at the place where they emerge. The location of new pseudopods is not random but highly ordered. Two types of pseudopodia may be formed: frequent splitting of an existing pseudopod, or the occasional extension of a de novo pseudopod at regions devoid of recent pseudopod activity. Split-pseudopodia are extended at approximately 60 degrees relative to the previous pseudopod, mostly as alternating Right/Left/Right steps leading to relatively straight zigzag runs. De novo pseudopodia are extended in nearly random directions thereby interrupting the zigzag runs. Persistence of cell movement is based on the ratio of split versus de novo pseudopodia. We identify PLA2 and cGMP signaling pathways that modulate this ratio of splitting and de novo pseudopodia, and thereby regulate the dispersal of cells. The observed ordered extension of pseudopodia in the absence of external cues provides a fundamental insight into the coordinated movement of cells, and might form the basis for movement that is directed by internal or external cues.

Figure 1. Pseudopod extensions.

A. Dictyostelium cells extend two types of pseudopodia, split and de novo. Left: Y-shape split. An existing pseudopod splits in two that are both protruded. Finally, the left pseudopod is retracted while the right pseudopod survives. Middle: One-way split. A protrusion is formed from the basis of an existing pseudopod; the cytoplasm flows into this new pseudopod, but not in the existing pseudopod. Right: De novo pseudopod. A slender protrusion is formed at an area of the cell that did not exhibit pseudopod activity in the previous two minutes. The cytoplasm flows into this new pseudopod. The images are at 8 s interval. The diagrams below the confocal images depict the pseudopod as arrow with the contour of the cell in the upper image. B. Track of a cell moving during 14 minutes in buffer (see movie S1 in supplemental information). The grey area indicates the contour of the cell during this movement. The arrows show the pseudopodia. As presented in figure 3, split pseudopodia are often alternating right/left leading to relatively straight path, while de novo pseudopodia are in random directions causing a change of direction.

Figure 2. Timing of pseudopod formation.

A. Schematic of the experiment. The two arrows indicate the start and finish of two pseudopodia. Panels B and D are probability frequency distributions of growth time and pseudopod interval, respectively, determined for 896 pseudopodia. Split and de novo pseudopodia have similar growth time (C) and pseudopod interval (E; sp = split, dn = de novo); data are means and SEM. Panel F presents the time point at which a new pseudopod starts during or after growth of the present pseudopod (1 means that the new pseudopod starts at the moment that the present pseudopod stops growth). Data are binned in 0.1 intervals. The grey bars indicate the probability that the next pseudopod will start during the indicated interval (see text for equation). The probability for a random start is given by (bin interval)x(mean t2)/(mean t1) = 0.1×12.9/15.7 = 0.082. The results show that the start of a new pseudopod is inhibited during growth of the present pseudopod, but is transiently activated immediately after the stop of the present pseudopod.

Figure 3. Direction of pseudopod extension.

A. Schematic of the experiment. Series of split pseudopodia were analyzed in which the present pseudopod is either a split or a de novo pseudopod. Angle 1 is the angle between the present pseudopod and the previous pseudopod. B and C, probability frequency distribution of angle 1 showing bimodal distribution for split pseudopodia with mean of about 55 degrees, and a broad distribution for de novo pseudopodia with a mean of 100 degrees. D–F, presents the angle of two subsequent pseudopodia, and shows that split-split exhibit a bias towards alternating steps (RL and LR) versus consecutive hops (RR and LL). De novo pseudopodia do not exhibit a right/left bias. The data of panel F are the means and SD of 16 cells. Panel G presents the autocorrelation of angle 1 with the angles of subsequent pseudopodia; the error bars indicate the SEM with n = 196 for split and n = 190 for de novo pseudopodia. The angle of a split pseudopod is negatively correlated with the angle of the following pseudopodia during 6 splits at a significance ***P<0.001; **P<0.01; *P<0.05. The angle of a de novo pseudopod is not correlated with the subsequent split pseudopodia.

Figure 4. Pseudopodia are extended perpendicular to cell curvature.

A. The angle θ between the present pseudopod and the previous pseudopod is plotted versus the distance d between the start of the present pseudopod and the tip of the previous pseudopod, as indicated in the inset. The lines represent the theoretical curves for pseudopodia that are extended perpendicular to a circle (purple with radius 5 µm) or an ellipsoid (green ). B. The angle α was determined that is formed by the direction of the pseudopod and the tangent to the cell boundary at the position of pseudopod emergence. Panel B shows the frequency distribution, while panel C presents the means and SEM of 306 split and 69 de novo pseudopodia. The angle α is statistically not significantly different from 90 degrees.

Figure 5. Pseudopod behavior of signaling mutants.

Wild-type cells (WT), pi3k1/2-null, gc-null, pla2-null and sgc/pla2-null cells were starved for 5 hours. The frequency of split and de novo pseudopodia is presented, as well as the ratio of split/de novo pseudopodia. The data shown are the means and SEM of 7 to 12 cells (*, significantly different from WT at P<0.01).

Figure 6. Dispersion of wild type and mutant cells.

Movies of 5 h starved wild type and mutant cells were recorded in 2.5 mM caffeine to inhibit cAMP signaling. Long cell tracks of at least 20 minutes were analyzed. Panels A–D show the tracks of 10 cells during 15 min; the grey circle indicates the average dispersal. Panel E shows the dispersal during time interval t; the symbols indicate the measured data, and the curves are the fit of the data to the equation of persistent movement (see text). The fitted parameters for speed (S) and persistence time (P) are presented in panel F; the error bars represent the 95% confidence limit (*, significantly different from WT at P<0.01).

Figure 7. Schematics of pseudopod extension in Dictyostelium.

A. A pseudopod timer initiates the extension of a new pseudopod every ∼15 seconds. Depending on the activity of PLA2 and guanylyl cyclase, this pseudopod is formed by splitting of an existing pseudopod or formed de novo on the cell body. The combination of pseudopodia being extended perpendicular to the cell surface, with distance and Left/Right bias is responsible for the relatively straight zig-zag trajectory of split pseudopodia and the random direction of a de novo pseudopod as indicated in panel B. Panel C shows a ‘model’ cell that has extended a pseudopod to the left, and is going to extend a new pseudopod. The model cell was constructed by separately averaging 30 pseudopodia and cell bodies (see discussion). The model pseudopod has a length of 5 µm, which is 6 µm via the perimeter; the cell body has a length of ∼11 µm, which is 14 µm via the perimeter. The length of the lines is proportional to the probability of pseudopod extension per micrometer. D. The probability that a new pseudopod is extended at different distances from the tip of this model cell was determined, and is expressed as % per µm perimeter of the model cell. E. The probability that the new pseudopod is extended to the right or left was calculated for the pseudopodia that emerged at different distances from the tip of the left-going pseudopod. The line segments that are drawn perpendicular to the model cell indicate the probability that a pseudopod is extended at that position. This pseudopod projection map suggests that amoeboid movement in the absence of external cues is orchestrated by mechanisms that inhibit pseudopodia in the cell body, and promote pseudopodia by splitting of the present pseudopod, but not at the tip, and not at the left side of a left-going pseudopod.