Young's modulus of elasticity of Schlemm's canal endothelial cells

Abstract

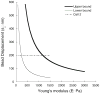
Schlemm's canal (SC) endothelial cells are likely important in the physiology and pathophysiology of the aqueous drainage system of the eye, particularly in glaucoma. The mechanical stiffness of these cells determines, in part, the extent to which they can support a pressure gradient and thus can be used to place limits on the flow resistance that this layer can generate in the eye. However, little is known about the biomechanical properties of SC endothelial cells. Our goal in this study was to estimate the effective Young's modulus of elasticity of normal SC cells. To do so, we combined magnetic pulling cytometry of isolated cultured human SC cells with finite element modeling of the mechanical response of the cell to traction forces applied by adherent beads. Preliminary work showed that the immersion angles of beads attached to the SC cells had a major influence on bead response; therefore, we also measured bead immersion angle by confocal microscopy, using an empirical technique to correct for axial distortion of the confocal images. Our results showed that the upper bound for the effective Young's modulus of elasticity of the cultured SC cells examined in this study, in central, non-nuclear regions, ranged between 1,007 and 3,053 Pa, which is similar to, although somewhat larger than values that have been measured for other endothelial cell types. We compared these values to estimates of the modulus of primate SC cells in vivo, based on images of these cells under pressure loading, and found good agreement at low intraocular pressure (8-15 mm Hg). However, increasing intraocular pressure (22-30 mm Hg) appeared to cause a significant increase in the modulus of these cells. These moduli can be used to estimate the extent to which SC cells deform in response to the pressure drop across the inner wall endothelium and thereby estimate the extent to which they can generate outflow resistance.

Fig. 1

Overview of ocular anatomy in aqueous humor drainage. Reproduced from Ethier et al. (2004) with permission of Elsevier. Middle panel modified from Hogan et al. (1971) with permission of Elsevier

Fig. 2

Inverted motorized microscope with bead-pulling setup including video camera (A), electric micromanipulator (B) and magnetic microneedle assembly; inset shows details of (C) with cell culture

Fig. 3

Horizontal magnetic force on bead as a function of distance from the tip of the microneedle. Solid line is best exponential fit

Fig. 4

a Phase contrast image of an SC cell with a bead (black arrow) attached to it. b fluorescence microscopy image of same cell showing actin labeling with rhodamine-phalloidin (Alexa Fluor 546, Molecular Probes). Note that there may be a second cell immediately adjacent to the cell of interest in this image

Fig. 5

The left panel shows a schematic of an x – z plane of a bead partially embedded in a cell, while the right panel shows the axially distorted view of this bead as imaged by confocal microscopy. α is the half immersion angle. D_a is the section diameter of the bead. z_c and z_a are the z-coordinates of the bead center and the apical surface of the cell, respectively, while $z_a^{\prime }$ is the distorted z-coordinate of the apical surface of the cell

Fig. 6

Domain used in finite element modeling showing a bead embedded in a cylindrical region of cytoplasm with a radius of 10 μm. In this model shown, the half-immersion angle is 98°

Fig. 7

Displacement (squares) of the bead attached to cell 2 resulting from magnetic pulling, initiated at time zero. The line is a best fit to these data for times >0 using Eq. (2). The initial bead displacement due to the pulling is approximately 200 nm, corresponding to the elastic response of the cell to the pulling. This is typical of the response of the beads due to magnetic pulling

Fig. 8

Spectrum of half-immersion angles measured from fourteen 4 μm fluorescent beads attached to SC cells. The beads selected for the measurement were at least 10 μm from the edge of the cell, and were not in the nuclear region

Fig. 9

Results of parametric studies on cell thickness, showing computed bead displacements as a function of cell thickness. The half immersion angles (α) were 60°, 84°, and 98°, corresponding to the minimum, average and maximum measured values, respectively. Young’s modulus of the cell was assumed to be 1,000 Pa. Lines shown are best fit to the equation s = A − Be^−w/C, where w is cell thickness, s is bead displacement and A, B and C are fitting constants

Fig. 10

Results of parametric studies showing how computed initial bead displacement (s₀) varies with the Young’s modulus of the cell (E, in Pa), for both the upper and lower bound cases. The initial displacement (s₀) of cell 2 measured from bead pulling experiment is also indicated in the figure (horizontal line). From this measured displacement, we deduce an upper bound and lower bound on E for this cell. See text for definition of upper and lower bound cases

Fig. 11

Section view of the computed strain field (maximum principal strain) around the bead for the minimum half immersion angle (60°, a) and the maximum half immersion angle (98°, b). Black arrows indicate the direction of pulling force in this section. The section plane passes through the bead center, and is perpendicular to the cell surface. Cell thickness is 3 μm, and the Young’s modulus is 1,000 Pa. The scale bar in b is 3 μm in length

Fig. 12

Inner wall of Schlemm’s canal of enucleated human eye perfused at 8 mm Hg. GV giant vacuole; SC Schlemm’s canal; ECM extracellular matrix; N cell nuclei. Reproduced from Ethier (2002) with permission of Elsevier