Dynamics of Positional Enrichment: Theoretical Development and Application to Carbon Labeling in Zymomonas mobilis
- PMID: 19412323
- PMCID: PMC2572007
- DOI: 10.1016/j.bej.2007.12.003
Dynamics of Positional Enrichment: Theoretical Development and Application to Carbon Labeling in Zymomonas mobilis
Abstract
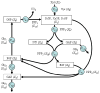
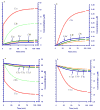
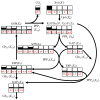
Positional enrichment analysis has become an important technique for assessing detailed flux distributions and the fates of specific atoms in metabolic pathway systems. The typical approach to positional enrichment analysis is performed by supplying specifically labeled substrate to a cell system, letting the system reach steady state, and measuring where label had arrived and accumulated. The data are then evaluated mathematically with the help of a linear stoichiometric flux distribution model. While this procedure has proven to yield new and valuable insights, it does not address the transient dynamics between providing label and its ultimate steady-state distribution, which is often of great interest to the experimentalist (pulse labeling experiments). We show here that an extension of a recent mathematical method for dynamic labeling analysis is able to shed light on these transitions, thereby revealing insights not obtained with traditional positional enrichment analyses. The method traces the dynamics of one or more carbons through fully regulated metabolic pathways, which, in principle, may be arbitrarily complex. After a brief review of the earlier method and description of the theoretical extension, we illustrate the method with an analysis of the pentose phosphate pathway in Zymomonas mobilis, which has been used for traditional positional enrichment analyses in the past. We show how different labeling schemes result in distinctly different transients, which nevertheless eventually lead to a steady-state labeling profile that coincides exactly with the corresponding profile from traditional analysis. Thus, over the domain of commonality, the proposed method leads to results equivalent to those from state-of-the-art existing methods. However, these steady-state results constitute only a small portion of the insights obtainable with the proposed method. Our method can also be used as an "inverse" technique for elucidating the topology and regulation of pathway systems, if appropriate time series data are available. While such dynamic data are still rather rare, they are now being generated with increasing frequency and we believe it is desirable, and indeed necessary, to accompany this trend with an adequate, rigorous method of analysis.
Figures

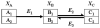




References
-
- Wiechert W. 13C metabolic flux analysis. Metab Eng. 2001;3:195–206. - PubMed
-
- Wiechert W, Mollney M, Petersen S, de Graaf AA. A universal framework for 13C metabolic flux analysis. Metab Eng. 2001;3:265–83. - PubMed
-
- Zupke C, S G. Modeling of Isotope Distributions and Intracellular Fluxes in Metabolic Networks Using Atom Mapping Matrixes. Biotechnology Progress. 1994;10:489–498.
-
- Eisenreich W, Bacher A. Elucidation of biosynthetic pathways by retrodictive/predictive comparison of isotopomer patterns determined by NMR spectroscopy. Genet Eng (N Y) 2000;22:121–53. - PubMed
-
- Wittmann C. Metabolic flux analysis using mass spectrometry. Adv Biochem Eng Biotechnol. 2002;74:39–64. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
