Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2009 May;45(3):850-67.
doi: 10.1037/a0014939.

Early math matters: kindergarten number competence and later mathematics outcomes

Nancy C Jordan  1 , David Kaplan, Chaitanya Ramineni, Maria N Locuniak
Affiliations

Early math matters: kindergarten number competence and later mathematics outcomes

Nancy C Jordan et al. Dev Psychol. 2009 May.

Abstract

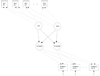
Children's number competencies over 6 time points, from the beginning of kindergarten to the middle of 1st grade, were examined in relation to their mathematics achievement over 5 later time points, from the end of 1st grade to the end of 3rd grade. The relation between early number competence and mathematics achievement was strong and significant throughout the study period. A sequential process growth curve model showed that kindergarten number competence predicted rate of growth in mathematics achievement between 1st and 3rd grades as well as achievement level through 3rd grade. Further, rate of growth in early number competence predicted mathematics performance level in 3rd grade. Although low-income children performed more poorly than their middle-income counterparts in mathematics achievement and progressed at a slower rate, their performance and growth were mediated through relatively weak kindergarten number competence. Similarly, the better performance and faster growth of children who entered kindergarten at an older age were explained by kindergarten number competence. The findings show the importance of early number competence for setting children's learning trajectories in elementary school mathematics.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Path diagram of sequential growth curve model for number competence (NC) from the beginning of kindergarten (K) through the middle of first grade and math achievement (Woodcock–Johnson III Achievement Tests–Mathematics [WJMath]) from the end of first grade through the end of third grade. Growth parameters for WJMath are regressed on the NC growth parameters (I = intercept, S = linear slope). Not all time points are shown because of space limitations.
Figure 2
Figure 2
Path diagram of sequential growth curve model for number competence (NC) from the beginning of kindergarten (K) through the middle of first grade and math achievement (Woodcock–Johnson III Achievement Tests–Mathematics [WJMath]) from the end of first grade through the end of third grade, with background variables of gender, income status, and kindergarten start age. Growth parameters for NC are regressed on the background variables, and the growth parameters for math achievement are regressed on the number competence growth parameters (I = intercept, S = linear slope). Not all time points are shown because of space limitations.
Figure 3
Figure 3
Observed and estimated means for (A) number competence (NC) raw scores and (B) Woodcock–Johnson III Achievement Tests–Mathematics (WJMath) raw scores. The x-axis reflects the waves of the study in months.
Figure 4
Figure 4
Estimated growth trajectories for (A) number competence (NC) raw scores and (B) Woodcock–Johnson III Achievement Tests–Mathematics (WJMath) raw scores by income status. The x-axis reflects the waves of the study in months.
Figure 5
Figure 5
Estimated growth trajectories for (A) Woodcock–Johnson III Applied Problems subtest (WJApp) raw scores and (B) Woodcock–Johnson III Calculation subtest (WJCalc) raw scores by income status. The x-axis reflects the waves of the study in months.
See this image and copyright information in PMC

References

    1. Arbuckle JL. Full information estimation in the presence of incomplete data. In: Marcoulides GA, Schumacker RE, editors. Advanced structural equation modeling: Issues and techniques. Mahwah, NJ: Erlbaum; 1996. pp. 243–277.
    1. Ashcraft MH. Cognitive arithmetic: A review of data and theory. Cognition. 1992;44:75–106. - PubMed
    1. Baroody AJ. Mastery of basic number combinations: Internalization of relationships or facts? Journal for Research in Mathematics Education. 1985;16(2):83–98.
    1. Baroody AJ. Children’s mathematical thinking: A developmental framework for preschool, primary, and special education teachers. New York: Teachers College Press; 1987.
    1. Baroody AJ, Rosu L. Adaptive expertise with basic addition and subtraction combinations. Paper presented at the annual meeting of the American Educational Research Association; San Francisco. 2006.

Publication types