Grain boundaries exhibit the dynamics of glass-forming liquids

Abstract

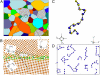
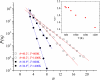
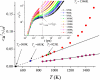
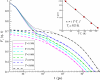
Polycrystalline materials are composites of crystalline particles or "grains" separated by thin "amorphous" grain boundaries (GBs). Although GBs have been exhaustively investigated at low temperatures, at which these regions are relatively ordered, much less is known about them at higher temperatures, where they exhibit significant mobility and structural disorder and characterization methods are limited. The time and spatial scales accessible to molecular dynamics (MD) simulation are appropriate for investigating the dynamical and structural properties of GBs at elevated temperatures, and we exploit MD to explore basic aspects of GB dynamics as a function of temperature. It has long been hypothesized that GBs have features in common with glass-forming liquids based on the processing characteristics of polycrystalline materials. We find remarkable support for this suggestion, as evidenced by string-like collective atomic motion and transient caging of atomic motion, and a non-Arrhenius GB mobility describing the average rate of large-scale GB displacement.

Fig. 1.

Illustration of string-like cooperative atomic motion within a GB. (A) Schematic microstructure of polycrystalline metal. Different colors indicate the individual grains having different orientations, and the black line segments represent GBs. (B) Equilibrium boundary structure projected onto the x–z plane for a θ = 40.23° [010] general tilt boundary at T = 900 K (x, y, and z axes are lab-fixed Cartesian coordinates, whereas [100], [010], and [001] refer to crystallographic axes). Upper and lower grains rotate relatively to each other by 40.23° along the common tilt axis [010]. The misorientation angle θ = 40.23° does not correspond to a special Σ value [Σ refers to the ratio of the volume of the coincidence site lattice (CSL) to the volume of crystal lattice]. The atoms are colored according to their coordination numbers q (orange, q = 12; others, q < 12). The simulation cell was chosen to have the GB plane normal to the z axis. (C) Representative string within GB plane. Yellow and blue spheres represent the atoms at an initial time t = 0 and a later time, t*. (D) Snapshot of string-like cooperative motion within the GB region at T = 900 K at Δt = t*. The rectangular box illustrates the simulation cell in the x–y plane. Biaxial strain ε_xx and ε_yy are applied to x–y plane to induce driving force that arises from the elastic energy difference between two grains, as shown in the diagram above the box.

Fig. 2.

Temporal evolution of the average boundary position at eight different temperatures. (Inset) Logarithm of the boundary mobility as a function of T [open circles versus 1/T (top axis) compare the data to an Arrhenius relationship, whereas the filled circles compare to the VF equation (bottom axis)]. The nonlinearity of the Arrhenius plot indicates that this relationship does not apply to GB mobility data.

Fig. 3.

String-length distribution function P(n) for θ = 36.9° boundary (Σ GB) and θ = 40.2° boundary (non-Σ GB) at 800 and 1,400 K. (Inset) Average string length 〈n〉 as a function of T for the GB, illustrating the growth of the scale of collective atomic motion after cooling. The scale of 〈n〉 at a corresponding reduced temperature is similar to that of previous simulation observations on GF liquids (9, 23).

Fig. 4.

DWF 〈u²〉 as a function of T for the GB and crystal. The solid red circles represent the DWF for GB, and the solid pink circles indicate the DWF for the lower grain. We observe that 〈u²〉 for the GB atomic motion (upper curve) is substantially larger than the scale of atomic motion in the grain (lower curve), with 〈u²〉 in the grain only obtaining a value comparable to the Lindemann value for temperatures near T_m = 1,621 K (18). The VF temperature T₀, determined from the M(T) data in Eq. 2, nearly coincides with the T at which 〈u²〉 extrapolates to 0. The temperature T_A = 1,546 K approximates the onset of the supercooling regime and was also determined from the M(T) data in Fig. 2 (see SI). The crossover temperature T_c is determined from the GB fluid structural relaxation time (see Fig. 5), and T_g is estimated by the condition 〈u²〉/σ² ≈ 0.125, where σ is the interatomic distance in the crystal, a Lindemann condition for glass formation (33). For the crystal grain, 〈u²〉 shows linear dependence over the entire T range. However, for GB, 〈u²〉 varies nearly linearly with T (harmonic localization) at low temperatures, but for T > T_c the harmonic approximation no longer applies. (Inset) 〈r²(t)〉 data from which 〈u²〉 ≡ 〈r²(t₀)〉 was determined. The vertical broken line indicates the inertial decorrelation time, t₀ (30).

Fig. 5.

The self-intermediate scattering function for GB particles in the T range of 1,050 and 1,150 K (defined in the text). The dashed curves are a fit of the stretched exponential relation, F_s(q,t) ∝ exp[−(t/τ)^β] to the long-time data, where the short-time decay arises from the inertial atomic dynamics. (Inset) A power fit of τ to T − T_c, where T_c and γ are adjustable parameters as in previous measurements and simulations.