Balance point characterization of interstitial fluid volume regulation

Abstract

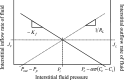
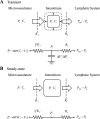
The individual processes involved in interstitial fluid volume and protein regulation (microvascular filtration, lymphatic return, and interstitial storage) are relatively simple, yet their interaction is exceedingly complex. There is a notable lack of a first-order, algebraic formula that relates interstitial fluid pressure and protein to critical parameters commonly used to characterize the movement of interstitial fluid and protein. Therefore, the purpose of the present study is to develop a simple, transparent, and general algebraic approach that predicts interstitial fluid pressure (P(i)) and protein concentrations (C(i)) that takes into consideration all three processes. Eight standard equations characterizing fluid and protein flux were solved simultaneously to yield algebraic equations for P(i) and C(i) as functions of parameters characterizing microvascular, interstitial, and lymphatic function. Equilibrium values of P(i) and C(i) arise as balance points from the graphical intersection of transmicrovascular and lymph flows (analogous to Guyton's classical cardiac output-venous return curves). This approach goes beyond describing interstitial fluid balance in terms of conservation of mass by introducing the concept of inflow and outflow resistances. Algebraic solutions demonstrate that P(i) and C(i) result from a ratio of the microvascular filtration coefficient (1/inflow resistance) and effective lymphatic resistance (outflow resistance), and P(i) is unaffected by interstitial compliance. These simple algebraic solutions predict P(i) and C(i) that are consistent with reported measurements. The present work therefore presents a simple, transparent, and general balance point characterization of interstitial fluid balance resulting from the interaction of microvascular, interstitial, and lymphatic function.

Fig. 1.

Graphical representation of the balance point concept applied to interstitial fluid flow. Continuous line represents the Starling-Landis relationship (Eq. 2) (41, 47), which predicts that as interstitial pressure (P_i) increases, transmicrovascular flow into the interstitium (J_V) decreases. The dotted line represents the Drake-Laine relationship (Eq. 4) (12), which predicts that as P_i increases, lymph flow from the interstitium (J_L) increases. Their intercepts represent equilibrium, where flow into the interstitium is equal to flow out of the interstitium (i.e., J_v = J_L). Dashed lines represent the steady-state values of P_i, J_L, and J_V, explicitly expressed by Eq. 8a. Intercepts and slopes are related to effective fluid-driving pressures and resistances to fluid flow. 1/K_f is the effective resistance to flow into the interstitium and R_L is the effective lymphatic resistance. P_c − ασ(C_c − C_i) represents the total effective pressure forcing fluid into the interstitium, where P_c is the capillary hydrostatic pressure and C_c − C_i is the difference between capillary and interstitial protein concentrations. P_out − P_p represents the total effective pressure hindering flow from the interstitium, where P_out is the lymphatic system outlet pressure (presumably central venous pressure) and P_p is the effective lymphatic pumping pressure.

Fig. 2.

Changes in interstitial fluid volume and pressure in response to a step change in capillary pressure. Illustrated are the results of numerically solving Eqs. 2–7, assuming the parameter values in Table I. Values of interstitial compliance, ΔV/ΔP_i, affect the rate at which the system comes to steady state, as well as the steady-state interstitial fluid volume. A 10-fold increase in interstitial compliance results in ∼6-fold increase in time required to reach steady state and ∼1.5-fold increase in the steady-state volume. Interstitial compliance has no impact on steady-state interstitial fluid pressure.

Fig. 3.

Data originally reported in Lund et al. (43) was derived from a 40% burn injury in skin, which caused a rapid increase in interstitial compliance. The resulting interstitial fluid pressure (P_i) dropped rapidly, which is normalized here by the peak negative value (P_imin = −31 mmHg). The curve represents simulation of the effect of rapidly increasing interstitial compliance on interstitial fluid pressure found by numerically solving Eqs. 2–7. The set of model parameters was chosen such that Eq. 8 reproduced the reported steady-state interstitial fluid pressure before the burn injury (approximately −1.6 mmHg). The value of interstitial compliance was chosen to reproduce the reported value of P_imin. The resulting model parameters were P_c = 16 mmHg, C_c = 58 mg/ml, σ = 0.62, P_p = 20 mmHg, P_out = 2 mmHg, K_f = 0.02 ml/100g·mmHg·min, and R_L = 66 mmHg·min/ml·100 g. Increase in interstitial compliance causes interstitial fluid pressure to rapidly drop, and then recover to baseline values following an exponential time course (time constant, ≈45 min).

Fig. 4.

Representation of interstitial fluid pressure (P_i) regulation in terms of both fluid compartments and an electrical analogy under transient (A) and steady-state conditions (B). With the electrical analogy, inlet resistance is equivalent to the inverse of the microvascular filtration coefficient (1/K_f), outlet resistance is equivalent to the effective lymphatic resistance (R_L), and capacitance is equivalent to the interstitial compliance (ΔV/ΔP_i). The effective inlet voltage is equivalent to [P_c − ασ(C_c − C_i)], which depends on capillary pressure (P_c), the reflection coefficient (σ), and the difference in capillary and interstitial protein concentrations (C_c − C_i). The effective outlet voltage is equivalent to (P_out − P_p), which depends on the lymphatic outlet pressure (P_out) and the effective lymphatic pump pressure (P_p). Under transient conditions, when interstitial inflow is greater than outflow, interstitial fluid volume increases. In this case, interstitial compliance affects transient changes in P_i. At steady state, inflow equals outflow, and interstitial compliance ceases to affect P_i. In this case, the ratio of 1/K_f and R_L determines whether P_i approaches microvascular driving pressure [P_c − ασ(C_c − C_i)] or effective lymphatic pumping pressure (P_out − P_p).

Fig. 5.

Illustration of the use of the graphical balance point analysis introduced in Fig. 1 to provide intuitive insight into interstitial fluid pressure regulation. Effect of changing various parameters and variables on interstitial fluid pressure (P_i), microvascular fluid filtration (J_V), and lymph outflow (J_L) is illustrated by a shift in the balance point from A to B. Subscripts indicate change from state 1 to state 2. A: increasing microvascular filtration coefficient (from K_f1 to K_f2) shifts the balance point from A to B and increases interstitial fluid pressure (from P_i1 to P_i2). B: increasing effective lymphatic resistance (from R_L1 to R_L2) shifts the balance point from A to B and increases interstitial fluid pressure (from P_i1 to P_i2). C: increasing capillary pressure (from P_c1 to P_c2) shifts the x-intercept from x₁ to x₂ and the balance point from A to B and results in higher interstitial fluid pressure (from P_i1 to P_i2). D: increasing lymphatic outlet pressure (from P_out1 to P_out2) shifts the x-intercept from x₁ to x₂ and the balance point from A to B and results in higher interstitial fluid pressure (from P_i1 to P_i2). E: concomitantly increasing K_f and R_L shifts the balance point from A to B and increases interstitial fluid pressure (from P_i1 to P_i2), but J_V and J_L are unaltered. F: simultaneously increasing K_f and decreasing R_L increases J_V and J_L, but maintains interstitial fluid pressure.

Fig. 6.

Microvascular protein extravasation rate (J_sV) estimation using the Taylor-Granger formulation (J_sV^TG) (Eq. 3) (56) is compared with the Kedem-Katchalsky formulation (J_sV^KK) (Eq. A1) (37) and the Manning formulation (J_sV^M) (Eq. A3) (44) assuming the Patlak-Hoffman formulation (J_sV^PH) (Eq. A2) (49) is ideal (7). A: ratio of errors as a function of J_V compares the Taylor-Granger formulation with the Kedem-Katchalsky formulation assuming C_i/C_c = 0.1, 0.5 and 0.9 (σ = 0.6, PS = 0.118). B: ratio of errors as a function of J_V compares the Taylor-Granger formulation with the Manning formulation assuming C_i/C_c = 0.1, 0.5, and 0.9 (σ = 0.6, PS = 0.118). R1 is reduced as C_i approaches C_c. However, it can be shown by algebraically reducing Eq. A4b that R2 is independent of C_c or C_i and is therefore not affected by changes in C_i/C_c. The fact that R1 >1 and R2 >1 with increasing J_V suggests that the Taylor-Granger formulation is the best approximation of the Patlak-Hoffman formulation.