Estimating parameters for generalized mass action models with connectivity information

Abstract

Background: Determining the parameters of a mathematical model from quantitative measurements is the main bottleneck of modelling biological systems. Parameter values can be estimated from steady-state data or from dynamic data. The nature of suitable data for these two types of estimation is rather different. For instance, estimations of parameter values in pathway models, such as kinetic orders, rate constants, flux control coefficients or elasticities, from steady-state data are generally based on experiments that measure how a biochemical system responds to small perturbations around the steady state. In contrast, parameter estimation from dynamic data requires time series measurements for all dependent variables. Almost no literature has so far discussed the combined use of both steady-state and transient data for estimating parameter values of biochemical systems.

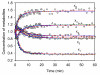
Results: In this study we introduce a constrained optimization method for estimating parameter values of biochemical pathway models using steady-state information and transient measurements. The constraints are derived from the flux connectivity relationships of the system at the steady state. Two case studies demonstrate the estimation results with and without flux connectivity constraints. The unconstrained optimal estimates from dynamic data may fit the experiments well, but they do not necessarily maintain the connectivity relationships. As a consequence, individual fluxes may be misrepresented, which may cause problems in later extrapolations. By contrast, the constrained estimation accounting for flux connectivity information reduces this misrepresentation and thereby yields improved model parameters.

Conclusion: The method combines transient metabolic profiles and steady-state information and leads to the formulation of an inverse parameter estimation task as a constrained optimization problem. Parameter estimation and model selection are simultaneously carried out on the constrained optimization problem and yield realistic model parameters that are more likely to hold up in extrapolations with the model.

Figure 1

Linear pathway. Metabolic reaction steps of the threonine pathway from aspartate in Escherichia coli. The dependent variables, x₁, x₂, x₃ and x₄, respectively denote the concentrations of aspartyl-P, D, L-aspartic β-semialdehyde, homoserine and O-phospho-homoserine. The independent variables, x₅, x₆, x₇, x₈, x₉ and x₁₀ represent ATP, ADP, NADPH, NADP, aspartate, threonine and Pi, respectively. (The model is called chassagnole2 in JWS web site).

Figure 2

Model validation for case I. Model validation using optimal estimates obtained with different computational approaches for an experiment with altered independent variables. Dashed curves represent the predicted profiles using the optimal estimates obtained from estimation without including the flux connectivity constraints. Solid curves represent the predicted profiles using the optimal estimates obtained from an estimation accounting for noise-free flux connectivity constraints. Dashed-dot-dot curves represent the predicted profiles using the optimal estimates obtained from an estimation accounting for 5% noise in the measured flux connectivity constraints. Data points are in silico observations. The independent variables [1.376, 0.179, 0.588, 0.630, 1.340, 3.490, 4.7500] were set 5% outside the training range.

Figure 3

Branched pathway with feedback. Metabolic map for branched pathway with five enzymes and feedback. (The model is called feedbackmoi in JWS web site.) x₁,..., x₅ are dependent variables, x₆, x₇ and x₈ are independent variables. Each product is fed back to regulate its corresponding pathway. Both x₁ and x₂ are also fed back to regulate the first reaction pathway.

Figure 4

Model validation for case II. Model validation using optimal estimates obtained with different computational approaches. Dashed curves represent the predicted profiles using optimal estimates obtained from estimation without accounting for flux connectivity constraints. Solid curves represent the predicted profiles using the optimal estimates obtained from an estimation accounting for noise-free flux connectivity constraints. Dashed-dot-dot curves represent the predicted profiles using the optimal estimates obtained from an estimation accounting for 5% noise in the measured flux connectivity constraints. Data points are in silico observations. The independent variables are set 5% outside the training range.