Patient-specific artery shrinkage and 3D zero-stress state in multi-component 3D FSI models for carotid atherosclerotic plaques based on in vivo MRI data

Abstract

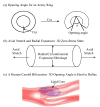
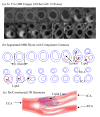
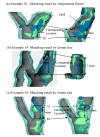
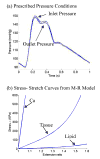
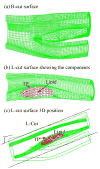
Image-based computational models for atherosclerotic plaques have been developed to perform mechanical analysis to quantify critical flow and stress/strain conditions related to plaque rupture which often leads directly to heart attack or stroke. An important modeling issue is how to determine zero stress state from in vivo plaque geometries. This paper presents a method to quantify human carotid artery axial and inner circumferential shrinkages by using patient-specific ex vivo and in vivo MRI images. A shrink-stretch process based on patient-specific in vivo plaque morphology and shrinkage data was introduced to shrink the in vivo geometry first to find the zero-stress state (opening angle was ignored to reduce the complexity), and then stretch and pressurize to recover the in vivo plaque geometry with computed initial stress, strain, flow pressure and velocity conditions. Effects of the shrink-stretch process on plaque stress/strain distributions were demonstrated based on patient-specific data using 3D models with fluid-structure interactions (FSI). The average artery axial and inner circumferential shrinkages were 25% and 7.9%, respectively, based on a data set obtained from 10 patients. Maximum values of maximum principal stress and strain increased 349.8% and 249% respectively with 33% axial stretch. Influence of inner circumferential shrinkage (7.9%) was not very noticeable under 33% axial stretch, but became more noticeable under smaller axial stretch. Our results indicated that accurate knowledge of artery shrinkages and the shrink-stretch process will considerably improve the accuracy of computational predictions made based on results from those in vivo MRI-based FSI models.

Keywords: Atherosclerosis; artery shrinkage; blood flow; carotid artery; fluid-structure interactions; vulnerable plaques.

Figure 1

Schematic drawing of 3 elements concerning zero stress state in 3D models. (a) Opening angle; (b) Axial shrinkage/stretch and circumferential shrinkage/expansion; (c) 3D reconstructed geometry of a human carotid plaque showing its nonuniform geometry and plaque components.

Figure 2

In vivo 3D MRI images of a human carotid plaque and re-constructed 3D geometry. (a) 16 MRI (T1) slices (S1–S16), slice spacing: 3mm. Each image shown here was cut from the whole neck image; (b) Segmented contour plots showing plaque components; (c) The reconstructed 3D geometry showing a lipid core.

Figure 3

In vivo and ex vivo MR images and 3D geometries of a human carotid plaque (Example #1) were compared to quantify axial and inner circumferential shrinkages. (a) In vivo MRI images and segmented contour plots; (b) Ex vivo MRI images and segmented contour plots; (c) 3D geometries and identified corresponding locations.

Figure 4

Three more examples showing plaque registration results, 3D view.

Figure 5

Pressure conditions and material stress-stretch curves used in the multi-component plaque FSI model. (a) Pressure conditions specified at the inlet (CCA) and outlet (ICA and ECA); (b) Stress-stretch curves derived from the modified Mooney-Rivlin model. The parameters are (c₂=0 for all materials; the unit for c₁ and D₁ is: dyn/cm²): vessel and fibrous tissue: c₁=368000, D₁=144000, D₂=2.0; lipid: c₁=20000, D₁=20000, D₂=1.5; Ca: C₁=3680000, D₁=1440000, D2=2.0.

Figure 6

Finite element meshes for the computational model showing different cut-surfaces. (a) Mesh for the solid domain showing the position of a bifurcation-cut (B-cut) surface; (b) A longitudinal-cut (L-cut) surface showing the lipid core and thin plaque cap; (c) Location of the L-cut surface.

Figure 7

Stress/strain distributions and flow characteristics from the 3D FSI model (Case 3, 10% axial stretch, 7.8 inner circumferential shrinkage), Pin=100 mmHg. (a) Plot of maximum principal stress (Stress-P₁) distribution on B-cut surface; (b) Plot of maximum principal strain (Strain-P₁) distribution on B-cut surface; (c) Stress-P₁ on L-cut surface; (d) Flow velocity reaching its maximum in the stenotic region; (e) Pressure band plot on L-cut surface; (f) Flow maximum shear stress band plot on L-cut surface showing a maximum at the stenosis throat.

Figure 8

Plots of Stress-P₁ distribution on L-cut surface from 6 case studies showing effects of axial stretch and circumferential shrinkage.

Figure 9

Plots of Strain-P₁ distribution on L-cut surface from 6 case studies showing effects of axial stretch and circumferential shrinkage.