Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2010 Jan;34(1):51-9.
doi: 10.1002/gepi.20434.

Discovering genetic ancestry using spectral graph theory

Ann B Lee  1 , Diana Luca, Lambertus Klei, Bernie Devlin, Kathryn Roeder
Affiliations

Discovering genetic ancestry using spectral graph theory

Ann B Lee et al. Genet Epidemiol. 2010 Jan.

Abstract

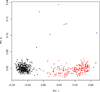
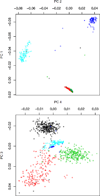
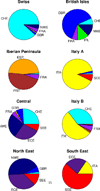
As one approach to uncovering the genetic underpinnings of complex disease, individuals are measured at a large number of genetic variants (usually SNPs) across the genome and these SNP genotypes are assessed for association with disease status. We propose a new statistical method called Spectral-GEM for the analysis of genome-wide association studies; the goal of Spectral-GEM is to quantify the ancestry of the sample from such genotypic data. Ignoring structure due to differential ancestry can lead to an excess of spurious findings and reduce power. Ancestry is commonly estimated using the eigenvectors derived from principal component analysis (PCA). To develop an alternative to PCA we draw on connections between multidimensional scaling and spectral graph theory. Our approach, based on a spectral embedding derived from the normalized Laplacian of a graph, can produce more meaningful delineation of ancestry than by using PCA. Often the results from Spectral-GEM are straightforward to interpret and therefore useful in association analysis. We illustrate the new algorithm with an analysis of the POPRES data [Nelson et al., 2008].

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
Principal components from PCA for Scenario 1. Subjects are self-identified as UK (black), Italian (red), and non-European (blue).
Fig. 2
Fig. 2
Principal components from the Spectral-GEM analysis of data from Scenario 1. Subjects are self-identified as UK (black), Italian (red), and non-European (blue).
Fig. 3
Fig. 3
Principal components 3–6 for data from Scenario 2. PC 1 and PC 2 are quite similar to the eigenvectors shown in Fig. 4. Subjects are self-identified as UK (black), Italian (red), Iberian Peninsula (green), African American (blue), and Indian (orange).
Fig. 4
Fig. 4
Principal components from the spectral graph approach for Scenario 2. Subjects are self-identified as UK (black), Italian (red), Iberian Peninsula (green), African American (blue), and Indian (orange).
Fig. 5
Fig. 5
Country membership by cluster for Scenario 3. Cluster labels and country groupings are defined in Table I. Cluster labels were derived from the majority country or country grouping membership.
Fig. 6
Fig. 6
Dendrogram for European clusters from Scenario 3.
See this image and copyright information in PMC

References

    1. Belkin M, Niyogi P. Laplacian eigenmaps and spectral techniques for embedding and clustering. Adv Neural Inf Process Sys. 2002;14
    1. Cavalli-Sforza L, Menozzi P, Piazza A. The History and Geography of Human Genes. Princeton: Princeton University Press; 1994.
    1. Chung F. Spectral graph theory. CBMS Regional Conference Series in Mathematics. 1992;92
    1. Epstein M, Allen A, GA S. A simple and improved correction for population stratification in case-control studies. Am J Hum Genet. 2007;73:921–930. - PMC - PubMed
    1. Heath SC, Gut IG, Brennan P, McKay JD, Bencko V, Fabianova E, Foretova L, Georges M, Janout V, Kabesch M, Krokan HE, Elvestad MB, Lissowska J, Mates D, Rudnai P, Skorpen F, Schreiber S, Soria JM, Syvnen AC, Meneton P, Herberg S, Galan P, Szeszenia-Dabrowska N, Zaridze D, Gnin E, Cardon LR, Lathrop M. Investigation of the fine structure of European populations with applications to disease association studies. Eur J Hum Genet. 2008;16:1413–1429. - PubMed

Publication types

MeSH terms