Computational models of the Notch network elucidate mechanisms of context-dependent signaling

Abstract

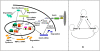
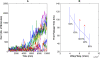
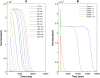
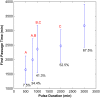
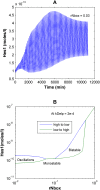
The Notch signaling pathway controls numerous cell fate decisions during development and adulthood through diverse mechanisms. Thus, whereas it functions as an oscillator during somitogenesis, it can mediate an all-or-none cell fate switch to influence pattern formation in various tissues during development. Furthermore, while in some contexts continuous Notch signaling is required, in others a transient Notch signal is sufficient to influence cell fate decisions. However, the signaling mechanisms that underlie these diverse behaviors in different cellular contexts have not been understood. Notch1 along with two downstream transcription factors hes1 and RBP-Jk forms an intricate network of positive and negative feedback loops, and we have implemented a systems biology approach to computationally study this gene regulation network. Our results indicate that the system exhibits bistability and is capable of switching states at a critical level of Notch signaling initiated by its ligand Delta in a particular range of parameter values. In this mode, transient activation of Delta is also capable of inducing prolonged high expression of Hes1, mimicking the "ON" state depending on the intensity and duration of the signal. Furthermore, this system is highly sensitive to certain model parameters and can transition from functioning as a bistable switch to an oscillator by tuning a single parameter value. This parameter, the transcriptional repression constant of hes1, can thus qualitatively govern the behavior of the signaling network. In addition, we find that the system is able to dampen and reduce the effects of biological noise that arise from stochastic effects in gene expression for systems that respond quickly to Notch signaling.This work thus helps our understanding of an important cell fate control system and begins to elucidate how this context dependent signaling system can be modulated in different cellular settings to exhibit entirely different behaviors.

Figure 1. Schematic of the Notch1-RBP-Jκ-Hes1 signaling network.

(A) Each arrow represents a term or event in the differential equation model including transcription, translation, mRNA and protein degradation, nuclear import, TF binding, receptor-ligand binding and receptor processing. (B) Schematic of the positive and negative feedback loops of the Notch1-RBP-Jk-Hes1 network. (-|) represents repression and (->) represents activation of target genes.

Figure 2. Bistability in Notch signaling.

(A) Deterministic Hes1 trajectories as a function of time for two different strengths of Delta signals given as a product of the Delta concentration and the rate constant of formation of NICD upon Delta-Notch binding (kfNcp*Delp = kDelp). These deterministic simulations were initiated using steady state values of the system under no Delta signal and at t = 750 minutes (indicated by vertical arrow) the input Delta signal was applied. (B) Hysteresis in the Notch1-Hes1 network, where Hes1 concentration can attain two possible steady states for an intermediate range of Delta inputs. The point of switching depends on whether the Delta signal is increasing or decreasing.

Figure 3. Stochastic simulations demonstrate spontaneous “OFF” to “ON” transitions.

(A) Representative stochastic Hes1 trajectories as a function of time after application of a constant Delta stimulus at 750 min at levels just below “ON” levels predicted by the deterministic model. Some Hes1 trajectories remain at low levels (“OFF” state) while others randomly switch state to higher levels (“ON” state). (B) First passage time (FPT) of stochastic trajectories for passage from “OFF” to “ON” state as a function of Delta signal strength in the bistable region. The mean and standard deviation of 40–60 runs in each case are plotted. The percentage of trajectories that switched to “ON” state under the given Delta signal is indicated below each data point. All points except those connected by the same letter (A) are statistically distinct (p<0.01, 2-tail t-test).

Figure 4. The Notch system exhibits bistability under stochastic simulations.

(A) Hes1 stochastic trajectories are shown during high Delta levels for 4000 minutes, following which the Delta signal is brought down to levels that failed to switch the state to “ON” when provided for a prolonged duration (kDelp = 4×10⁻⁴) in the deterministic model. All the trajectories remain in the “ON” state – corresponding to the region of bistability seen in the deterministic simulations. (B) Hes1 stochastic trajectories are shown after application of a high Delta signal for 4000 minutes, after which the Delta signal is brought down to 0. Some trajectories persist in the “ON” state.

Figure 5. Both input Delta signal strength and duration affect the output Hes1 expression levels.

(A) Effect of Delta signal duration on the Hes1 expression levels: a transient Delta signal of kfNcp*Delp = 5×10⁻³ was provided in the deterministic model for varying amounts of time ranging from 10 minutes to 3000 minutes, and the resulting Hes1 trajectories were simulated up to 15000 minutes. (B) The effect of Delta signal strength on Hes1 expression: a transient Delta signal of varying strengths (expressed as kDelp = kfNcp*Delp (min⁻¹)) was provided in the deterministic model for 100 minutes, and the resulting Hes1 were simulated up to 20000 minutes.

Figure 6. First passage time (FPT) for passage from “OFF” to “ON” state as a function of Delta signal duration in stochastic simulations.

The mean and standard deviation of >20 runs in each case are plotted. The percentage of trajectories that switched to the “ON” state under the given Delta signal is indicated below each data point. All points except those connected by the same letter (A,B,C) are statistically distinct (p<0.01, 2-tail t-test).

Figure 7. Bifurcation Analysis.

(A) Bifurcation analysis of how the switching points vary with the equilibrium binding constant (K_a) of NICD to RBP-Jk. Stronger interaction between NICD and RBP-Jk lowers the threshold of Delta signal required to turn the system ON. (B) Bifurcation analysis of how the switching points vary with the maximal transcription rate of Hes1 (V_maxh). A higher maximal transcription rate, indicating a stronger Hes1 promoter, also slightly shifts the region of bistability towards lower Delta signal strengths.

Figure 8. Effect of the repression constant of Hes1 (r_Nbox) on the Notch signaling network.

(A) At lower values or r_Nbox (higher repression constants for Hes1), the network predicts oscillations in Hes1 levels. As the value of r_Nbox is decreased to 0.03 and lower, the system exhibits stable oscillations. (B) At a fixed Delta signal strength of kDelp = 2×10⁻⁴, as the r_Nbox is progressively decreased, the response of Hes1 transitions from behaving as a bistable switch to a brief region of monostability to an oscillator.