Control and regulation of integrated mitochondrial function in metabolic and transport networks

Abstract

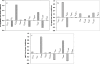
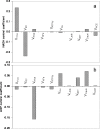
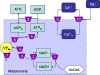
The pattern of flux and concentration control coefficients in an integrated mitochondrial energetics model is examined by applying a generalized matrix method of control analysis to calculate control coefficients, as well as response coefficients The computational model of Cortassa et al. encompasses oxidative phosphorylation, the TCA cycle, and Ca(2+) dynamics. Control of ATP synthesis, TCA cycle, and ANT fluxes were found to be distributed among various mitochondrial processes. Control is shared by processes associated with ATP/ADP production and transport, as well as by Ca(2+) dynamics. The calculation also analyzed the control of the concentrations of key regulatory ions and metabolites (Ca(2+), NADH, ADP). The approach we have used demonstrates how properties of integrated systems may be understood through applications of computational modeling and control analysis.

Keywords: Mitochondrial computational model; calcium dynamics; control by diffuse loops; distributed control; excitation-contraction coupling; metabolic control analysis; mitochondrial energetics.

Figure 1.

Control of metabolic fluxes in the ME model. The control coefficient by each of the steps of the ME model are represented for (a) the ATP synthase, (b) the TCA cycle, and (c) the ANT. See the legend of Scheme 1 for abbreviations. Panel (a) reprinted from Cortassa, S.; O’Rourke, B.; Winslow, R.L.; Aon, M.A. Control and regulation of mitochondrial energetics in an integrated model of cardiomyocyte function. Biophysical Journal 2009, 96, 2466 – 2478 with permission from Elsevier.

Figure 2.

(a) Control of NADH and ADP concentrations in the ME model. Represented are the control coefficients of NADH (a) and ADP (b), extracted from the computed matrix of metabolite concentration control coefficients.

Scheme 1.

Scheme of the model ECME subjected to control analysis. Processes accounted for by the ME model are numbered according to the following key: [Table: see text] The scheme shows mass transformation interactions between the state variables of the mitochondrial energetics (ME) model. In the model the TCA cycle starts from AcCoA, i.e. the common intermediary metabolite derived from sugars and fatty acids degradation, thus, not accounting for the activity of pyruvate dehydrogenase, one of the targets of Ca²⁺ regulation [23]. In the scheme, regulatory interactions were omitted for simplicity (see [8] for more details). State variables are indicated in rectangular (ion or metabolites) while boxes depict a light blue background when the state variables participate in conservation relationships (ATP/ADP, NAD⁺/NADH) or a dark blue background for ionic species. The hexagonal box denotes the input of carbon substrate that corresponds to a parameter in the model. Arrowheads point to the products of the numbered processes, whereas lines without arrowheads indicate inputs to those processes. The TCA cycle was considered as a single step in the stoichiometric matrix; however, for the quantification of the elasticity coefficients of the TCA cycle with respect to the intermediates, the disaggregated individual rate expressions and their dependence with respect to Ca²⁺ _m, NAD⁺, NADH, ADP_m, and ATP_m were taken into account. The individual elasticities were then added together to compute the overall elasticity of the TCA cycle (see [8] for details). ΔΨ_m correspond to the mitochondrial membrane potential.