Bet-hedging as an evolutionary game: the trade-off between egg size and number
- PMID: 19474039
- PMCID: PMC2817213
- DOI: 10.1098/rspb.2009.0500
Bet-hedging as an evolutionary game: the trade-off between egg size and number
Abstract
Bet-hedging theory addresses how individuals should optimize fitness in varying and unpredictable environments by sacrificing mean fitness to decrease variation in fitness. So far, three main bet-hedging strategies have been described: conservative bet-hedging (play it safe), diversified bet-hedging (don't put all eggs in one basket) and adaptive coin flipping (choose a strategy at random from a fixed distribution). Within this context, we analyse the trade-off between many small eggs (or seeds) and few large, given an unpredictable environment. Our model is an extension of previous models and allows for any combination of the bet-hedging strategies mentioned above. In our individual-based model (accounting for both ecological and evolutionary forces), the optimal bet-hedging strategy is a combination of conservative and diversified bet-hedging and adaptive coin flipping, which means a variation in egg size both within clutches and between years. Hence, we show how phenotypic variation within a population, often assumed to be due to non-adaptive variation, instead can be the result of females having this mixed strategy. Our results provide a new perspective on bet-hedging and stress the importance of extreme events in life history evolution.
Figures
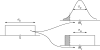
 , and σw, in the females’ ‘genome’. σb is the standard deviation in a uniform distribution with mean
, and σw, in the females’ ‘genome’. σb is the standard deviation in a uniform distribution with mean  and corresponds to between year variation in the mean propagule size produced by each female. Every year, each female will ‘choose’ a value of her mean propagule size (
and corresponds to between year variation in the mean propagule size produced by each female. Every year, each female will ‘choose’ a value of her mean propagule size ( ), and the distribution within the clutch around that mean has a standard deviation of σw, independently of whether she produces a clutch with normally or uniformly distributed propagule sizes. The dashed line corresponds to an arbitrary mmin, which varies from one time step to another. All propagule sizes smaller than mmin (grey area) will not survive.
), and the distribution within the clutch around that mean has a standard deviation of σw, independently of whether she produces a clutch with normally or uniformly distributed propagule sizes. The dashed line corresponds to an arbitrary mmin, which varies from one time step to another. All propagule sizes smaller than mmin (grey area) will not survive.

Comment in
-
Bet-hedging as an evolutionary game: the trade-off between egg size and number.Proc Biol Sci. 2010 Apr 22;277(1685):1149-51. doi: 10.1098/rspb.2009.1541. Epub 2009 Dec 16. Proc Biol Sci. 2010. PMID: 20018792 Free PMC article. No abstract available.
Similar articles
-
Spatial variation in egg size and egg number reflects trade-offs and bet-hedging in a freshwater fish.J Anim Ecol. 2012 Jul;81(4):806-17. doi: 10.1111/j.1365-2656.2012.01961.x. Epub 2012 Feb 6. J Anim Ecol. 2012. PMID: 22309288
-
Bet-hedging as an evolutionary game: the trade-off between egg size and number.Proc Biol Sci. 2010 Apr 22;277(1685):1149-51. doi: 10.1098/rspb.2009.1541. Epub 2009 Dec 16. Proc Biol Sci. 2010. PMID: 20018792 Free PMC article. No abstract available.
-
The evolution of different maternal investment strategies in two closely related desert vertebrates.Ecol Evol. 2017 Mar 31;7(9):3177-3189. doi: 10.1002/ece3.2838. eCollection 2017 May. Ecol Evol. 2017. PMID: 28480017 Free PMC article.
-
Bet-hedging--a triple trade-off between means, variances and correlations.Biol Rev Camb Philos Soc. 2012 Aug;87(3):742-55. doi: 10.1111/j.1469-185X.2012.00225.x. Epub 2012 Mar 10. Biol Rev Camb Philos Soc. 2012. PMID: 22404978 Review.
-
Evolutionary bet-hedging in the real world: empirical evidence and challenges revealed by plants.Proc Biol Sci. 2010 Oct 22;277(1697):3055-64. doi: 10.1098/rspb.2010.0707. Epub 2010 Jun 23. Proc Biol Sci. 2010. PMID: 20573624 Free PMC article. Review.
Cited by
-
Serotoninergic Modulation of Phototactic Variability Underpins a Bet-Hedging Strategy in Drosophila melanogaster.Front Behav Neurosci. 2021 Apr 16;15:659331. doi: 10.3389/fnbeh.2021.659331. eCollection 2021. Front Behav Neurosci. 2021. PMID: 33935664 Free PMC article.
-
Offspring mass variation in tree swallows: A case of bet-hedging?Ecosphere. 2019 Mar 7;10(3):e02607. doi: 10.1002/ecs2.2607. eCollection 2019 Mar. Ecosphere. 2019. PMID: 35865407 Free PMC article.
-
From endosymbionts to host communities: factors determining the reproductive success of arthropod vectors.Oecologia. 2017 Aug;184(4):859-871. doi: 10.1007/s00442-017-3906-4. Epub 2017 Jul 18. Oecologia. 2017. PMID: 28721523
-
Fidelity varies in the symbiosis between a gutless marine worm and its microbial consortium.Microbiome. 2022 Oct 22;10(1):178. doi: 10.1186/s40168-022-01372-2. Microbiome. 2022. PMID: 36273146 Free PMC article.
-
Fluctuating Environments Maintain Genetic Diversity through Neutral Fitness Effects and Balancing Selection.Mol Biol Evol. 2021 Sep 27;38(10):4362-4375. doi: 10.1093/molbev/msab173. Mol Biol Evol. 2021. PMID: 34132791 Free PMC article.
References
-
- Brown J. S., Venable D. L.1986Evolutionary ecology of seedbank annuals in temporally varying environments. Am. Nat. 127, 31–47 (doi:10.1086/284465) - DOI
-
- Charlesworth B.1971Selection in density-regulated populations. Ecology 52, 469–474 (doi:10.2307/1937629) - DOI
-
- Cohen D.1966Optimizing reproduction in a randomly varying environment. J. Theor. Biol. 12, 119–129 (doi:10.1016/0022-5193(66)90188-3) - DOI - PubMed
-
- Cooper W. S., Kaplan R. H.1982Adaptive ‘coin-flipping’: a decision-theoretical examination of natural selection for a random individual variation. J. Theor. Biol. 94, 135–151 (doi:10.1016/0022-5193(82)90336-8) - DOI - PubMed
-
- Crump M. L.1981Variation in propagule size as a function of environmental uncertainty for tree frogs. Am. Nat. 117, 724–737 (doi:10.1086/283755) - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

