Predators indirectly control vector-borne disease: linking predator-prey and host-pathogen models

Abstract

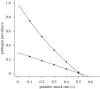
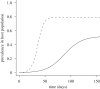
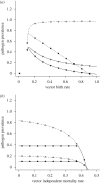
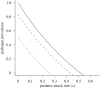
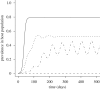
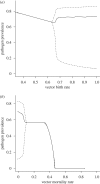
Pathogens transmitted by arthropod vectors are common in human populations, agricultural systems and natural communities. Transmission of these vector-borne pathogens depends on the population dynamics of the vector species as well as its interactions with other species within the community. In particular, predation may be sufficient to control pathogen prevalence indirectly via the vector. To examine the indirect effect of predators on vectored-pathogen dynamics, we developed a theoretical model that integrates predator-prey and host-pathogen theory. We used this model to determine whether predation can prevent pathogen persistence or alter the stability of host-pathogen dynamics. We found that, in the absence of predation, pathogen prevalence in the host increases with vector fecundity, whereas predation on the vector causes pathogen prevalence to decline, or even become extinct, with increasing vector fecundity. We also found that predation on a vector may drastically slow the initial spread of a pathogen. The predator can increase host abundance indirectly by reducing or eliminating infection in the host population. These results highlight the importance of studying interactions that, within the greater community, may alter our predictions when studying disease dynamics. From an applied perspective, these results also suggest situations where an introduced predator or the natural enemies of a vector may slow the rate of spread of an emerging vector-borne pathogen.

Figure 1.

Regions of stability in parameter space for each of the system equilibria as a function of vector birth rate (b_N) and predator attack rate (α). (a) When there is no predator in the system, the pathogen reproduction number, R₀, and pathogen persistence are a function of vector birth rate. (b) When a predator is added, the pathogen reproduction number and pathogen persistence depend on b_N and α. The solid line represents the R₀ = 1 isocline and the dashed line represents the P* = 0 isocline. The other model parameter values are H = 1, β_VH = 0.15, β_HV = 0.15, γ = 0.05, m_N = 0.1, d_N = 0.05, ε = 0.25 and m_P = 0.1.

Figure 2.

Pathogen prevalence in the host and vector populations as a function of the predator attack rate (α). Pathogen prevalence is measured as the proportion of infected hosts (I*/H) and vectors (V*/N*) in their respective populations at equilibrium. The other model parameter values are H = 1, β_VH = 0.15, β_HV = 0.15, γ = 0.05, b_N = 0.35, m_N = 0.1, d_N = 0.05, ε = 0.25, m_P = 0.1. (Filled squares, host population; filled triangles, vector population.)

Figure 3.

Model of an epidemic outbreak in the presence or absence of a predator. At t = 0, the host population is entirely susceptible and 1 per cent of the vector population is infectious. Parameter values are H = 1, β_VH = 0.15, β_HV = 0.15, γ = 0.05, b_N = 0.35, d_N = 0.05, m_N = 0.1, α = 0.2, ε = 0.25 and m_P = 0.1. R₀ = 2.54 when predator is absent and R₀ = 1.60 when predator is present at its equilibrium density. (Solid line, predator present; dashed line, predator absent.)

Figure 4.

(a) Pathogen prevalence, represented as the proportion of the host and vector population that is infected, as a function of the vector birth rate (b_N) either in the absence of predation (open symbols) or with the predator present at its equilibrium density (filled symbols). When b_N < m_N (m_N = 0.1), the vector population is absent at equilibrium, and by necessity the pathogen cannot persist. (b) Pathogen prevalence in the host and vector populations as a function of the non-predation vector mortality rate (m_N). In the absence of the predator, an increase in the vector mortality rate leads to a decrease in pathogen prevalence, while pathogen prevalence does not respond to an increase in vector mortality when a predator is present. The other model parameter values are H = 1, b_V = 0.5 (b only), β_VH = 0.15, β_HV = 0.15, γ = 0.05, d_N = 0.05, α = 0.2, ε = 0.25 and m_P = 0.1. (Open squares, predator absent—host population; open inverse triangles, predator absent—vector population; filled squares, predator present—host population; filled inverse triangles, predator present—vector population.)

Figure 5.

Disease prevalence as a function of vector productivity with varying rates of (a) disease-induced mortality (solid line, δ = 0; dashed line, δ = 0.01; dotted line, δ = 0.05; dot and dashed line, δ = 0.10) and (b) reductions in host fecundity (solid line, ρ = 1.0; dashed line, ρ = 0.5; dotted line, ρ = 0.25; dot and dashed line, ρ = 0). The other model parameter values are b_H = 0.20, m_H = 0.05, ϕ = 0.2, δ = 0, β_VH = 0.15, β_HV = 0.15, m_N = 0.1, d_N = 0.05, α = 0.2, ε = 0.25, m_P = 0.1, ρ = 1 (a only) and δ = 0 (b only).

Figure 6.

Disease prevalence in the host population as a function of predator attack rate (α) for three different host recovery rates (γ) with lifelong immunity for recovered individuals. The other model parameter values are H = 1, β_VH = 0.2, β_HV = 0.2, γ = 0.05, b_N = 0.35, m_N = 0.1, d_N = 0.05, ε = 0.25 and m_P = 0.1. (Solid line, γ = 0; dashed line, γ = 0.01; dotted line, γ = 0.05.)

Figure 7.

Model of an epidemic outbreak for different values of α′ for a predator with a type II functional response. At t = 0, the host population is entirely susceptible and 1 per cent of the vector population is infectious. Parameter values are H = 1, β_VH = 0.15, β_HV = 0.15, γ = 0.05, b_N = 0.35, d_N = 0.05, m_N = 0.1, ε = 0.25, m_P = 0.1 and f = 1. (Solid line, α′ = 0; dotted line, α′ = 0.4; dot and dashed line, α′ = 0.5; dashed line, α′ = 0.9.)

Figure 8.

(a) Pathogen prevalence, represented as the proportion of the host population that is infected, as a function of the vector birth rate (b_N) when the predator has a type II functional response. (b) Pathogen prevalence in the host population as a function of the non-predation vector mortality rate (m_N). Solid lines represent mean prevalence and dashed lines represent the minimum and maximum prevalence values when prevalence is cyclical. Parameter values are H = 1, β_VH = 0.15, β_HV = 0.15, γ = 0.05, b_N = 0.7 (b only), d_N = 0.05, m_N = 0.1 (a only), α′ = 0.5, ε = 0.25 m_P = 0.1 and f = 1.