A multivariate regression approach to association analysis of a quantitative trait network

Abstract

Motivation: Many complex disease syndromes such as asthma consist of a large number of highly related, rather than independent, clinical phenotypes, raising a new technical challenge in identifying genetic variations associated simultaneously with correlated traits. Although a causal genetic variation may influence a group of highly correlated traits jointly, most of the previous association analyses considered each phenotype separately, or combined results from a set of single-phenotype analyses.

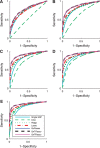
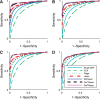
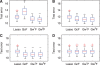
Results: We propose a new statistical framework called graph-guided fused lasso to address this issue in a principled way. Our approach represents the dependency structure among the quantitative traits explicitly as a network, and leverages this trait network to encode structured regularizations in a multivariate regression model over the genotypes and traits, so that the genetic markers that jointly influence subgroups of highly correlated traits can be detected with high sensitivity and specificity. While most of the traditional methods examined each phenotype independently, our approach analyzes all of the traits jointly in a single statistical method to discover the genetic markers that perturb a subset of correlated traits jointly rather than a single trait. Using simulated datasets based on the HapMap consortium data and an asthma dataset, we compare the performance of our method with the single-marker analysis, and other sparse regression methods that do not use any structural information in the traits. Our results show that there is a significant advantage in detecting the true causal single nucleotide polymorphisms when we incorporate the correlation pattern in traits using our proposed methods.

Availability: Software for GFlasso is available at http://www.sailing.cs.cmu.edu/gflasso.html.

Fig. 1.

Illustration of association analysis using phenotype correlation graph for asthma dataset.

Fig. 2.

Illustrations for multiple output regression with (A) lasso; (B) GFlasso; and (C) G_wFlasso.

Fig. 3.

ROC curves for comparison of association analysis methods with different sample size N. (A) N = 50; (B) N = 100; (C) N = 150; (D) N = 200; and (E) N = 250. The effect size is 0.5, and the threshold ρ for the phenotype network is set to 0.3. Note that the curves for G_cFlasso, G¹_wFlasso and G²_wFlasso almost entirely overlap.

Fig. 4.

ROC curves for comparison of association analysis methods with varying effect size. Effect size is (A) 0.3; (B) 0.5; (C) 0.8; and (D) 1.0. The sample size is 100, and the threshold ρ for the phenotype correlation graph is 0.1.

Fig. 5.

ROC curves for comparison of association analysis methods with different values of threshold (ρ) for the phenotype correlation network. (A) ρ = 0.1; (B) ρ = 0.3; (C) ρ = 0.5; and (D) ρ = 0.7. The sample size is 100, and the effect size is 0.8.

Fig. 6.

Comparison of association analysis methods in terms of phenotype prediction error. The threshold ρ for the phenotype correlation network is (A) ρ = 0.1; (B) ρ = 0.3; (C) ρ = 0.5; and (D) ρ = 0.7.

Fig. 7.

Results of association analysis by different methods based on a single simulated dataset. Effect size 0.8 and threshold ρ = 0.3 for the phenotype correlation graph are used. Bright pixels indicate large values. (A) The correlation coefficient matrix of phenotypes; (B) the edges of the phenotype correlation graph obtained at threshold 0.3 are shown as white pixels; (C) The true regression coefficients used in simulation. Rows correspond to SNPs and columns to phenotypes; (D) −log(P-value). Absolute values of the estimated regression coefficients are shown for ((E) ridge regression; (F) CCA; (G) lasso; (H) G_cFlasso; (I) G¹_wFlasso; and (J) G²_wFlasso.

Fig. 8.

Comparison of the computation time for lasso, G_cFlasso, G¹_wFlasso and G²_wFlasso. (A) Varying the number of SNPs with the number of phenotypes fixed at 10. The phenotype correlation graph at threshold ρ = 0.3 with 31 edges is used. (B) Varying the number of phenotypes with the number of SNPs fixed at 50. The phenotype networks are obtained using threshold ρ = 0.3. The number of edges in each phenotype network is 11, 34, 53, 88 and 142 for the number of phenotypes 10, 20, 30, 40 and 50, respectively.

Fig. 9.

Results for the association analysis of the asthma dataset. (A) Phenotype correlation matrix. (B) Phenotype correlation matrix thresholded at ρ = 0.7. (C) −log(P-value) from single-marker statistical tests using a single-phenotype analysis. Estimated β_k's for (D) ridge regression; (E) lasso; (F) G_cFlasso; (G) G¹_wFlasso; and (H) G²_wFlasso.