Psychometric approaches for developing commensurate measures across independent studies: traditional and new models

Abstract

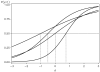
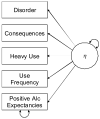
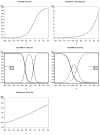
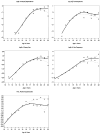
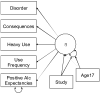
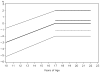
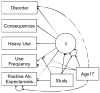
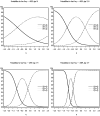
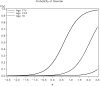
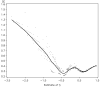
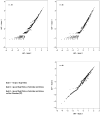
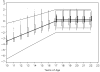
When conducting an integrative analysis of data obtained from multiple independent studies, a fundamental problem is to establish commensurate measures for the constructs of interest. Fortunately, procedures for evaluating and establishing measurement equivalence across samples are well developed for the linear factor model and commonly used item response theory models. A newly proposed moderated nonlinear factor analysis model generalizes these models and procedures, allowing for items of different scale types (continuous or discrete) and differential item functioning across levels of categorical and/or continuous variables. The potential of this new model to resolve the problem of measurement in integrative data analysis is shown via an empirical example examining changes in alcohol involvement from ages 10 to 22 years across 2 longitudinal studies.

Figure 1

Tracelines of four items in a 2-PL. Vertical droplines indicate item difficulties culties with values, from left to right, of -1, -.5, 0, and .75, with corresponding discriminations of .5, 1, .75, and 1.5.

Figure 2

Path diagram of nonlinear factor analysis model where the factor η measures alcohol involvement.

Figure 3

Relationships between each measured variable y and the latent alcohol involvement factor η.

Figure 4

Observed proportions/means of the indicator variables, submitted to link function transformation, plotted as a function of Age and Study (× = AFDP; ○ = AHBP); plots for Use Frequency and Heavy Use are based on proportions scoring 1 or 2 versus 0.

Figure 5

Path diagram for moderated nonlinear factor analysis model with age and study effects on the mean and variance of the Alcohol Involvement factor, η.

Figure 6

Estimated Age and Study differences in Alcohol Involvement: Bold lines indicate means, light lines indicate ± 2 standard deviations; solid lines indicate AFDP and dashed lines indicate AHBP.

Figure 7

Path diagram for moderated nonlinear factor analysis model with Age and Study effects on the factor mean and variance and on item parameters for indicators displaying DIF.

Figure 8

Tracelines for the Frequency of Use indicator demonstrating DIF as a function of Age and Study.

Figure 9

Tracelines for the Disorder indicator showing DIF by Age.

Figure 10

Standard errors for MAP factor score estimates obtained from the MNLFA model with DIF, as a function of the estimated factor score value.

Figure 11

MAP estimates obtained from models with and without age and study effects on the factor mean and variance and item parameters (DIF).

Figure 12

Boxplots of MAP factor scores obtained at each age for the two studies, shown in relation to the model implied means (bold lines) and ± two standard deviations (light lines): AFDP indicated with white boxes and solid lines, AHBP indicated with gray boxes and dashed lines.