Evolution of resource cycling in ecosystems and individuals
- PMID: 19486519
- PMCID: PMC2698886
- DOI: 10.1186/1471-2148-9-122
Evolution of resource cycling in ecosystems and individuals
Abstract
Background: Resource cycling is a defining process in the maintenance of the biosphere. Microbial communities, ranging from simple to highly diverse, play a crucial role in this process. Yet the evolutionary adaptation and speciation of micro-organisms have rarely been studied in the context of resource cycling. In this study, our basic questions are how does a community evolve its resource usage and how are resource cycles partitioned?
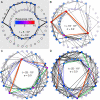
Results: We design a computational model in which a population of individuals evolves to take up nutrients and excrete waste. The waste of one individual is another's resource. Given a fixed amount of resources, this leads to resource cycles. We find that the shortest cycle dominates the ecological dynamics, and over evolutionary time its length is minimized. Initially a single lineage processes a long cycle of resources, later crossfeeding lineages arise. The evolutionary dynamics that follow are determined by the strength of indirect selection for resource cycling. We study indirect selection by changing the spatial setting and the strength of direct selection. If individuals are fixed at lattice sites or direct selection is low, indirect selection result in lineages that structure their local environment, leading to 'smart' individuals and stable patterns of resource dynamics. The individuals are good at cycling resources themselves and do this with a short cycle. On the other hand, if individuals randomly change position each time step, or direct selection is high, individuals are more prone to crossfeeding: an ecosystem based solution with turbulent resource dynamics, and individuals that are less capable of cycling resources themselves.
Conclusion: In a baseline model of ecosystem evolution we demonstrate different eco-evolutionary trajectories of resource cycling. By varying the strength of indirect selection through the spatial setting and direct selection, the integration of information by the evolutionary process leads to qualitatively different results from individual smartness to cooperative community structures.
Figures


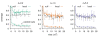
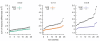
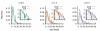


Similar articles
-
Eco-evolutionary feedbacks in community and ecosystem ecology: interactions between the ecological theatre and the evolutionary play.Philos Trans R Soc Lond B Biol Sci. 2009 Jun 12;364(1523):1629-40. doi: 10.1098/rstb.2009.0012. Philos Trans R Soc Lond B Biol Sci. 2009. PMID: 19414476 Free PMC article.
-
Beyond simple adaptation: Incorporating other evolutionary processes and concepts into eco-evolutionary dynamics.Ecol Lett. 2023 Sep;26 Suppl 1:S16-S21. doi: 10.1111/ele.14197. Ecol Lett. 2023. PMID: 37840027
-
Coexistence in a variable environment: eco-evolutionary perspectives.J Theor Biol. 2013 Dec 21;339:14-25. doi: 10.1016/j.jtbi.2013.05.005. Epub 2013 May 20. J Theor Biol. 2013. PMID: 23702333
-
Toward an integration of evolutionary biology and ecosystem science.Ecol Lett. 2011 Jul;14(7):690-701. doi: 10.1111/j.1461-0248.2011.01627.x. Epub 2011 May 9. Ecol Lett. 2011. PMID: 21554512 Review.
-
The ecology, evolution, impacts and management of host-parasite interactions of marine molluscs.J Invertebr Pathol. 2015 Oct;131:177-211. doi: 10.1016/j.jip.2015.08.005. Epub 2015 Sep 2. J Invertebr Pathol. 2015. PMID: 26341124 Review.
Cited by
-
Klebsiella oxytoca facilitates microbiome recovery via antibiotic degradation and restores colonization resistance in a diet-dependent manner.Nat Commun. 2025 Jan 9;16(1):551. doi: 10.1038/s41467-024-55800-y. Nat Commun. 2025. PMID: 39789003 Free PMC article.
-
Microbial Communities Are Well Adapted to Disturbances in Energy Input.mSystems. 2016 Sep 13;1(5):e00117-16. doi: 10.1128/mSystems.00117-16. eCollection 2016 Sep-Oct. mSystems. 2016. PMID: 27822558 Free PMC article.
-
Spatial vulnerability: bacterial arrangements, microcolonies, and biofilms as responses to low rather than high phage densities.Viruses. 2012 May;4(5):663-87. doi: 10.3390/v4050663. Epub 2012 Apr 26. Viruses. 2012. PMID: 22754643 Free PMC article.
-
Beware batch culture: Seasonality and niche construction predicted to favor bacterial adaptive diversification.PLoS Comput Biol. 2017 Mar 30;13(3):e1005459. doi: 10.1371/journal.pcbi.1005459. eCollection 2017 Mar. PLoS Comput Biol. 2017. PMID: 28358919 Free PMC article.
-
Insights into resource consumption, cross-feeding, system collapse, stability and biodiversity from an artificial ecosystem.J R Soc Interface. 2017 Jan;14(126):20160816. doi: 10.1098/rsif.2016.0816. J R Soc Interface. 2017. PMID: 28100827 Free PMC article.
References
-
- Treves DS, Manning S, J A. Repeated evolution of an acetate-crossfeeding polymorphism in long-term populations of Escherichia coli. Mol Biol Evol. 1998;15:789–797. - PubMed
-
- Porcher E, Tenaillon O, Godelle B. From metabolism to polymorphism in bacterial populations: a theoretical study. Evolution. 2001;55:2181–2193. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

