Modelling HIV immune response and validation with clinical data

Abstract

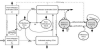
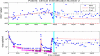
A system of ordinary differential equations is formulated to describe the pathogenesis of HIV infection, wherein certain features that have been shown to be important by recent experimental research are incorporated in the model. These include the role of CD4+ memory cells that serve as a major reservoir of latently infected cells, a critical role for T-helper cells in the generation of CD8 memory cells capable of efficient recall response, and stimulation by antigens other than HIV. A stability analysis illustrates the capability of this model in admitting multiple locally asymptotically stable (locally a.s.) off-treatment equilibria.We show that this more biologically detailed model can exhibit the phenomenon of transient viremia experienced by some patients on therapy with viral load levels suppressed below the detection limit. We also show that the loss of CD4+ T-cell help in the generation of CD8+ memory cells leads to larger peak values for the viral load during transient viremia. Censored clinical data is used to obtain parameter estimates. We demonstrate that using a reduced set of 16 free parameters, obtained by fixing some parameters at their population averages, the model provides reasonable fits to the patient data and, moreover, that it exhibits good predictive capability. We further show that parameter values obtained for most clinical patients do not admit multiple locally a.s off-treatment equilibria. This suggests that treatment to move from a high viral load equilibrium state to an equilibrium state with a lower (or zero) viral load is not possible for these patients.

Keywords: HIV; censored data; immune response; inverse problems; model prediction; multiple equilibria.

Figure 1

Flow chart of model (2.1) with compartments as described in Table 1. Solid black arrows indicate death/clearance, solid gray arrows indicate birth/input. PI and RTI denote protease inhibitor and reverse transcriptase inhibitor, respectively.

Figure 2

Phase diagram showing equilibrium attained as a function of the initial viral load ν and the parameter a_T. It should be emphasized that this plot is only applicable for the particular initial condition (0, 0, 1400, 0, ν, 0, 0.01, 0).

Figure 3

Phase diagram showing equilibrium attained as a function of the initial viral load ν and the parameter a_A. Initial conditions for simulations, corresponding to the uninfected equilibrium EQ₁, are calculated for each value of a_A. Note that a_T = 8 × 10⁻³ day⁻¹ for these simulations.

Figure 4

(a) Activation rate a_A(t) by a non-HIV antigen. The duration of the infection is 30 days; (b) Viral load V_I(t) (solid line), censored data level (horizontal dashed line), and infection start and stop times (vertical dash-dot lines).

Figure 5

Model dynamics with ε₁ = 0.7, ε₂ = 0, and the values of all the other parameters as specified in Table 2. Activation rate by a non-HIV antigen a_A(t) is as depicted in Fig. 4(a). Vertical dashed lines indicate the start and stop times of the non-HIV infection.

Figure 6

(a) Activation rate by non-HIV antigens a_A(t). The duration of each infection is 30 days, with the first beginning on day 20 and the second on day 80; (b) Viral load V_I(t) (solid line) and censor data level (horizontal dashed line).

Figure 7

(a) Activation rate by non-HIV antigens a_A(t). The duration of each infection is 30 days, with the first beginning on day 20 and the second on day 200; (b) Viral load V_I(t) (solid line) and censor data level (horizontal dashed line).

Figure 8

Model dynamics with ε₁ = 0.7, ε₂ = 0, and the values of all the other parameters as specified in Table 2. Activation rate by a non-HIV antigen a_A(t) is as depicted in Fig. 7(a). Vertical dashed lines indicate the start and stop times of the non-HIV infections for this example. The vertical dotted line indicates the start time (80 days) of the second infection in Fig. 6.

Figure 9

(a) The effect of K_γ on the “healthy” infected (EQ₂) values of the V_I (circles), E₁ (crosses), and E₂ (asterisks) compartments. Equilibrium values correspond to the case ε₁ = 0.7, ε₂ = 0, a_A = 0, and the values of all other parameters as specified in Table 5; (b) Relative change of V_I (circles), E₁ (crosses), and E₂ (asterisks) compartments as a function of K_γ.

Figure 10

Clinical data (‘x’) for CD4 T-cells (upper graph) and viral load (lower graph). Also included are the model results with parameters estimated from full data (dash-dot line) or half longitudinal data (solid line). Dark and gray circles denote the predicted censored data values for the full and half longitudinal data, respectively. The vertical line in the middle of the graph delineates between the two halves of the longitudinal data. A solid line along the x-axis in the upper figure indicates periods when the patient is on HAART treatment, while a dashed line indicates off-treatment periods.

Figure 11

Clinical data (‘x’) for CD4 T-cells (upper graph) and viral load (lower graph). Also included are the model results with parameters estimated from full data (dash-dot line) or half longitudinal data (solid line). Dark and gray circles denote the predicted censored data values for the full and half longitudinal data, respectively. The vertical line in the middle of the graph delineates between the two halves of the longitudinal data. A solid line along the x-axis in the upper figure indicates periods when the patient is on HAART treatment, while a dashed line indicates off-treatment periods.

Figure 12

Clinical data (‘x’) for CD4 T-cells (upper graph) and viral load (lower graph). Also included are the model results with parameters estimated from full data (dash-dot line) or half longitudinal data (solid line). Dark and gray circles denote the predicted censored data values for the full and half longitudinal data, respectively. The vertical line in the middle of the graph delineates between the two halves of the longitudinal data. A solid line along the x-axis in the upper figure indicates periods when the patient is on HAART treatment, while a dashed line indicates off-treatment periods.

Figure 13

Clinical data (‘x’) for CD4 T-cells (upper graph) and viral load (lower graph). Also included are the model results with parameters estimated from full data (dash-dot line) or half longitudinal data (solid line). Dark and gray circles denote the predicted censored data values for the full and half longitudinal data, respectively. The vertical line in the middle of the graph delineates between the two halves of the longitudinal data. A solid line along the x-axis in the upper figure indicates periods when the patient is on HAART treatment, while a dashed line indicates off-treatment periods.

Figure 14

CD4 T-cells (upper graph) and viral load (lower graph).

Figure 15

CD4 T-cells (upper graph) and viral load (lower graph).

Figure 16

CD4 T-cells (upper graph) and viral load (lower graph).

Figure 17

CD4 T-cells (upper graph) and viral load (lower graph).

Figure 18

CD4 T-cells (upper graph) and viral load (lower graph).

Figure 19

CD4 T-cells (upper graph) and viral load (lower graph).

Figure 20

CD4 T-cells (upper graph) and viral load (lower graph).

Figure 21

CD4 T-cells (upper graph) and viral load (lower graph).

Figure 22

CD4 T-cells (upper graph) and viral load (lower graph).

Figure 23

CD4 T-cells (upper graph) and viral load (lower graph).