Dancing volvox: hydrodynamic bound states of swimming algae
- PMID: 19518757
- PMCID: PMC4833199
- DOI: 10.1103/PhysRevLett.102.168101
Dancing volvox: hydrodynamic bound states of swimming algae
Abstract
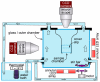
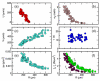
The spherical alga Volvox swims by means of flagella on thousands of surface somatic cells. This geometry and its large size make it a model organism for studying the fluid dynamics of multicellularity. Remarkably, when two nearby Volvox colonies swim close to a solid surface, they attract one another and can form stable bound states in which they "waltz" or "minuet" around each other. A surface-mediated hydrodynamic attraction combined with lubrication forces between spinning, bottom-heavy Volvox explains the formation, stability, and dynamics of the bound states. These phenomena are suggested to underlie observed clustering of Volvox at surfaces.
Figures


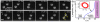
References
-
- van Leeuwenhoek A. Phil. Trans. R. Soc. London. 1700;22:509.
-
- Linnaeus C. Systema Naturae. 10th ed Impensis Laurentii Salvii; Stockholm: 1758. p. 820.
-
- Weismann A. Essays Upon Heredity and Kindred Biological Problems. Clarendon Press; Oxford: 1891.
-
- Kirk DL. Volvox: Molecular-genetic Origins of Multicellularity and Cellular Differentiation. Cambridge University Press; Cambridge: 1998.
-
- Kirk DL. BioEssays. 2005;27:299. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
