Unlimited multistability in multisite phosphorylation systems
- PMID: 19536158
- PMCID: PMC2859978
- DOI: 10.1038/nature08102
Unlimited multistability in multisite phosphorylation systems
Abstract
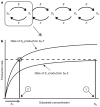
Reversible phosphorylation on serine, threonine and tyrosine is the most widely studied posttranslational modification of proteins. The number of phosphorylated sites on a protein (n) shows a significant increase from prokaryotes, with n </= 7 sites, to eukaryotes, with examples having n >/= 150 sites. Multisite phosphorylation has many roles and site conservation indicates that increasing numbers of sites cannot be due merely to promiscuous phosphorylation. A substrate with n sites has an exponential number (2(n)) of phospho-forms and individual phospho-forms may have distinct biological effects. The distribution of these phospho-forms and how this distribution is regulated have remained unknown. Here we show that, when kinase and phosphatase act in opposition on a multisite substrate, the system can exhibit distinct stable phospho-form distributions at steady state and that the maximum number of such distributions increases with n. Whereas some stable distributions are focused on a single phospho-form, others are more diffuse, giving the phospho-proteome the potential to behave as a fluid regulatory network able to encode information and flexibly respond to varying demands. Such plasticity may underlie complex information processing in eukaryotic cells and suggests a functional advantage in having many sites. Our results follow from the unusual geometry of the steady-state phospho-form concentrations, which we show to constitute a rational algebraic curve, irrespective of n. We thereby reduce the complexity of calculating steady states from simulating 3 x 2(n) differential equations to solving two algebraic equations, while treating parameters symbolically. We anticipate that these methods can be extended to systems with multiple substrates and multiple enzymes catalysing different modifications, as found in posttranslational modification 'codes' such as the histone code. Whereas simulations struggle with exponentially increasing molecular complexity, mathematical methods of the kind developed here can provide a new language in which to articulate the principles of cellular information processing.
Figures
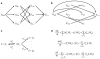


References
-
- Walsh CT. Posttranslational Modification of Proteins. Roberts and Company; 2006.
-
- Cohen P. The role of reversible protein phosphorylation in health and disease. Eur. J. Biochem. 2001;268:5001–5010. - PubMed
-
- Cohen P. The regulation of protein function by multisite phosphorylation — a 25 year update. Trends Biochem. Sci. 2000;25:596–601. - PubMed
-
- Holmberg CI, Tran SEF, Eriksson JE, Sistonen L. Multisite phosphorylation provides sophisticated regulation of transcription factors. Trends Biochem. Sci. 2002;27:619–627. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

