On the biomechanics of heart valve function
- PMID: 19540499
- PMCID: PMC2746960
- DOI: 10.1016/j.jbiomech.2009.05.015
On the biomechanics of heart valve function
Abstract
Heart valves (HVs) are fluidic control components of the heart that ensure unidirectional blood flow during the cardiac cycle. However, this description does not adequately describe the biomechanical ramifications of their function in that their mechanics are multi-modal. Moreover, they must replicate their cyclic function over an entire lifetime, with an estimated total functional demand of least 3x10(9) cycles. The focus of the present review is on the functional biomechanics of heart valves. Thus, the focus of the present review is on functional biomechanics, referring primarily to biosolid as well as several key biofluid mechanical aspects underlying heart valve physiological function. Specifically, we refer to the mechanical behaviors of the extracellular matrix structural proteins, underlying cellular function, and their integrated relation to the major aspects of valvular hemodynamic function. While we focus on the work from the author's laboratories, relevant works of other investigators have been included whenever appropriate. We conclude with a summary of important future trends.
Conflict of interest statement
The authors have no conflict of interest, financial or otherwise, that would affect their impartiality of this work.
Figures


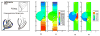

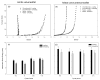


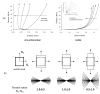





References
-
- Adamczyk MM, Vesely I. Characteristics of compressive strains in porcine aortic valves cusps. J Heart Valve Dis. 2002;11(1):75–83. - PubMed
-
- Aikawa E, Whittaker P, Farber M, Mendelson K, Padera RF, Aikawa M, Schoen FJ. Human semilunar cardiac valve remodeling by activated cells from fetus to adult: implications for postnatal adaptation, pathology, and tissue engineering. Circulation. 2006;113(10):1344–52. - PubMed
-
- Arts T, Meerbaum S, Reneman R, Corday E. Stresses in the closed mitral valve: a model study. J Biomech. 1983;16(7):539–47. - PubMed
-
- Bairati A, DeBiasi S. Presence of a smooth muscle system in aortic valve leaflets. Anatomy and Embryology. 1981;161(3):329–40. - PubMed
-
- Bellhouse BJ, Bellhouse FH. Fluid mechanics of the mitral valve. Nature. 1969;224:615–618. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
- R01 HL68816/HL/NHLBI NIH HHS/United States
- HL073021/HL/NHLBI NIH HHS/United States
- R01 HL052009/HL/NHLBI NIH HHS/United States
- R01 HL089750/HL/NHLBI NIH HHS/United States
- R01 HL068816/HL/NHLBI NIH HHS/United States
- R01 HL063026/HL/NHLBI NIH HHS/United States
- HL089750/HL/NHLBI NIH HHS/United States
- HL071814/HL/NHLBI NIH HHS/United States
- HL520009/HL/NHLBI NIH HHS/United States
- EB003392 T32/EB/NIBIB NIH HHS/United States
- HL63026/HL/NHLBI NIH HHS/United States
- R01 HL071814/HL/NHLBI NIH HHS/United States
- R56 HL071814/HL/NHLBI NIH HHS/United States
- R01 HL073021/HL/NHLBI NIH HHS/United States
- T32 EB003392/EB/NIBIB NIH HHS/United States
- R01 HL070969/HL/NHLBI NIH HHS/United States
LinkOut - more resources
Full Text Sources
Other Literature Sources

