Direct observation of an ensemble of stable collapsed states in the mechanical folding of ubiquitin

Abstract

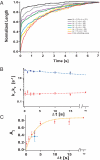
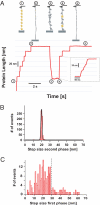
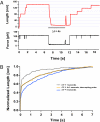
Statistical theories of protein folding have long predicted plausible mechanisms for reducing the vast conformational space through distinct ensembles of structures. However, these predictions have remained untested by bulk techniques, because the conformational diversity of folding molecules has been experimentally unapproachable. Owing to recent advances in single molecule force-clamp spectroscopy, we are now able to probe the structure and dynamics of the small protein ubiquitin by measuring its length and mechanical stability during each stage of folding. Here, we discover that upon hydrophobic collapse, the protein rapidly selects a subset of minimum energy structures that are mechanically weak and essential precursors of the native fold. From this much reduced ensemble, the native state is acquired through a barrier-limited transition. Our results support the validity of statistical mechanics models in describing the folding of a small protein on biological timescales.

Fig. 1.

Identification of a weakly stable ensemble of collapsed conformations in the folding of ubiquitin. (A) We repeatedly unfold and extend a ubiquitin polyprotein at 110 pN and then reduce the force to 10 pN for a varying amount of time, Δt, to trigger folding. First the polyprotein elongates in well defined steps of 20 nm, because each protein in the chain unfolds at a high force. Upon quenching the force the extended protein collapses. We probe the state of the collapsed polypeptide by raising the force back to 110 pN and measuring the kinetics of the protein elongation. (B) After full collapse we observe that the protein becomes segregated into 2 distinct ensembles: The first is identified by a fast heterogeneous elongation made of multiple sized steps (Inset); the second corresponds to well defined steps of 20 nm that identify fully folded proteins. The ratio between these 2 states of the protein depends on Δt. Longer values of Δt favor the native ensemble.

Fig. 2.

Kinetics of conversion from collapsed to native conformations. Extended proteins were allowed to collapse for a duration Δt, and then were reextended at a high force to probe the nature of the collapsed ensemble. (A) For a given Δt, averages of 30–60 extensions are well described by double exponential fits (dotted lines). The fits measure the unraveling rate constant of the weakly stable collapsed state, k_1, and the fully stable protein, k_2, and their relative amplitude A₁ and A₂. (B) k₁ is 40-fold faster than k₂, while both are nearly independent of Δt (blue and red squares, respectively). The rate k₂ = 0.5 s⁻¹ is in close agreement with the kinetics of unfolding of native ubiquitin. (C) The fraction of native conformations, A₂, increased exponentially with Δt (dotted line) with a rate constant of k_f = 0.3 s⁻¹. The blue data point highlights that the formation of native contacts occurs only after the folded length is reached (SI Appendix, Fig. S2).

Fig. 3.

A broad ensemble of transition states characterizes the collapsed conformations. The test pulse in a typical refolding trajectory of a single polyubiquitin protein with a short collapse time Δt is composed of 2 distinct regimes. In both regimes the polyprotein elongates in a stepwise manner. A stepwise extension under force identifies a conformation that extends by overcoming an energy barrier (A). The precise location of the transition state within the structure determines the number of amino acids that will extend after the barrier is crossed. The native state is marked by stepwise extensions that are narrowly distributed around 20 nm 19.7 ± 0.6 nm (n = 607) (A and B), signifying a well defined transition state. By contrast, the majority of the collapsed conformations extend in steps that cover a wide range of values up to 29 nm, with a reduced number as high as 62 nm (C and A Inset). The distribution of step sizes of the collapsed conformations is largely contained within the contour length of a single ubiquitin monomer (dashed line in C). The observation of individual collapsed states is limited to the time resolution of our feedback response, 5–10 ms.

Fig. 4.

The collapsed conformations are mechanically labile and exhibit a distance to the transition state similar to that of the native form. We use a 3-pulse protocol (F₁ to F₃ in A) to measure the force-dependent extension of both the collapsed and native conformation ensembles. After a standard force-quench sequence (F₁ and F₂), the force-dependent rate of extension of the collapsed conformations k₁ is measured by varying the force of F₃ within the range 30–70 pN, whereas the force dependent rate of unfolding of the native conformations, k₂, is studied by varying F₁ within the range 90–190 pN. Remarkably, the time-course of unraveling the ensemble of collapsed states when pulled at F₃ = 50 pN is greatly slowed down, taking place in ≈2 s in this particular trajectory. The length trace corresponding to the force pulse F₃ captures only the unraveling trajectories of individual collapsed states as revealed by their different unraveling step sizes (the last step in the recording at ≈10 s, marked with an arrow, features ≈25 nm) and to the vanishingly small probability of observing a step corresponding to the unfolding of the native state when ubiquitin is pulled at 50 pN. (B) A logarithmic plot of the average rate of unraveling of the collapsed conformations (triangles) as a function of the pulling force. These rates were measured from the weighted average of biexponential fits to the unraveling time course of 25–50 recordings at each force (SI Appendix, Fig. S8A). We fit an Arrhenius term to the unraveling rate of the collapsed conformations k₁(F) (triangles) to estimate the average size of the activation energy barrier, 〈ΔG₁〉, and distance to the transition state, Δx₁, of the collapsed conformations in PBS solution, yielding a Δx₁ ≈ 0.2 Å. To describe the rate of unfolding of the native state (k₂) we use single exponential fits to the average time-course of unfolding at each particular force as a practical first approximation (SI Appendix, Fig. S8B). As we have demonstrated before, a single exponential fit captures ≈81% of the unfolding events and thus represents a reasonable measure of the unfolding rate (45). Fitting the Arrhenius term to the unfolding rate of the native state k₂(F) (circles) yields a similar distance to the transition state, Δx₂ = 1.6 Å (dotted black line). Red and green dotted lines correspond to the fit of the experimental data to the analytical equation derived from Kramers's theory (35) assuming a cusp-like and a linear-cubic energy profile, respectively (SI Appendix, Table S1). The blue horizontal line represents the limit in the rate resolution for experiments conducted with cantilevers with a spring constant of 15 pN/nm.

Fig. 5.

Collapsed conformations are necessary precursors of the native state. (A) After a regular force-quench, we use a brief force pulse (60 pN; 100 ms) to disrupt the ensemble of collapsed conformations during their conversion to the native ensemble. (B) We averaged 51 extensions at 110 pN after the interruption of the refolding process at Δt = 4s (orange) and compared its effect to the average extension time-course obtained for uninterrupted Δt = 5 s (blue) and Δt = 1 s (gray) trajectories. It is clear that the short force pulse delays the recovery of the mechanically stable native conformations.