A model of transluminal flow of an anti-HIV microbicide vehicle: Combined elastic squeezing and gravitational sliding

Abstract

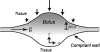
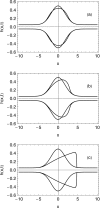
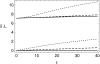
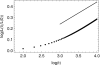
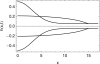
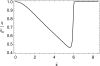
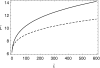
ELASTOHYDRODYNAMIC LUBRICATION OVER SOFT SUBSTRATES IS OF IMPORTANCE IN A NUMBER OF BIOMEDICAL PROBLEMS: From lubrication of the eye surface by the tear film, to lubrication of joints by synovial fluid, to lubrication between the pleural surfaces that protect the lungs and other organs. Such flows are also important for the drug delivery functions of vehicles for anti-HIV topical microbicides. These are intended to inhibit transmission into vulnerable mucosa, e.g., in the vagina. First generation prototype microbicides have gel vehicles, which spread after insertion and coat luminal surfaces. Effectiveness derives from potency of the active ingredients and completeness and durability of coating. Delivery vehicle rheology, luminal biomechanical properties, and the force due to gravity influence the coating mechanics. We develop a framework for understanding the relative importance of boundary squeezing and body forces on the extent and speed of the coating that results. A single dimensionless number, independent of viscosity, characterizes the relative influences of squeezing and gravitational acceleration on the shape of spreading in the Newtonian case. A second scale, involving viscosity, determines the spreading rate. In the case of a shear-thinning fluid, the Carreau number also plays a role. Numerical solutions were developed for a range of the dimensionless parameter and compared well with asymptotic theory in the limited case where such results can be obtained. Results were interpreted with respect to trade-offs between wall elasticity, longitudinal forces, bolus viscosity, and bolus volume. These provide initial insights of practical value for formulators of gel delivery vehicles for anti-HIV microbicidal formulations.

Figure 1

Definition sketch of the vaginal canal. The introitus is to the right. See also anatomical figures in Ref. .

Figure 2

Profiles of the shape of the bolus at dimensionless times t=0 s and t=20 s for (a) W=0.118 (e.g., case 6), (b) W=1.18 (e.g., cases 1 and 3), and (c) W=5.9 (e.g., cases 2 and 4). Volume is 2 ml.

Figure 3

Evolution of the dimensionless length of the bolus (four times the standard deviation in x of the bolus height; upper curves) and mean dimensionless longitudinal displacement (lower curves) as functions of dimensionless time for W=0.118 (solid), 1.18 (dashed), and 5.9 (dotted), i.e., cases 1, 2 and 4, and 6. Volume is 2 ml.

Figure 4

Evolution of the spread length of the bolus divided by the length due to squeezing only (W=0) as a function of W. The relative length is shown at dimensionless times t=0, 1000, 5000, and 10 000 s, reading up from bottom. The volume of the bolus is 2 ml.

Figure 5

A comparison against the asymptotic spread rate ∝t^1∕5 (upper line) and the simulation results scaled by the original bolus length (lower set of points). Volume is 4 ml.

Figure 6

Profiles of the shape of the right half of the C20V bolus at times t=0 s and $\tilde{t}=600\mathrm{s}$.

Figure 7

Effective shear viscosity at the epithelial surface vs $\tilde{x}$ (cm) for the C20V bolus at $\tilde{t}=600\mathrm{s}$.

Figure 8

Profiles of the shape of the right half of the K20S bolus at times t=0 s and $\tilde{t}=600\mathrm{s}$.

Figure 9

Effective shear viscosity at the epithelial surface vs $\tilde{x}$ (cm) for the K20S bolus at $\tilde{t}=600\mathrm{s}$.

Figure 10

Spread length vs time for the C20V and K20S (dashed) cases.