Waves and patterning in developmental biology: vertebrate segmentation and feather bud formation as case studies
- PMID: 19557684
- PMCID: PMC4188424
- DOI: 10.1387/ijdb.072493rb
Waves and patterning in developmental biology: vertebrate segmentation and feather bud formation as case studies
Abstract
In this article we will discuss the integration of developmental patterning mechanisms with waves of competency that control the ability of a homogeneous field of cells to react to pattern forming cues and generate spatially heterogeneous patterns. We base our discussion around two well known patterning events that take place in the early embryo: somitogenesis and feather bud formation. We outline mathematical models to describe each patterning mechanism, present the results of numerical simulations and discuss the validity of each model in relation to our example patterning processes.
Figures


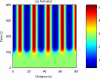
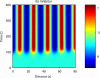
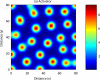
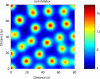

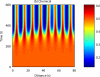

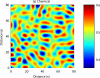
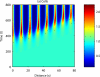

Comment in
-
Pattern formation today.Int J Dev Biol. 2009;53(5-6):653-8. doi: 10.1387/ijdb.082594cc. Int J Dev Biol. 2009. PMID: 19557673 Free PMC article. Review.
References
-
- AFFOLTER M, WEIJER CJ. Signaling to cytoskeletal dynamics during chemotaxis. Dev. Cell. 2005;9:19–34. - PubMed
-
- AKAM M. Making stripes inelegantly. Nature. 1989;341:282–283. - PubMed
-
- BAKER RE. D.Phil. University of Oxford; 2005. Periodic pattern formation in developmental biology: a study of the mechanisms underlying somitogenesis.
-
- BAKER RE, SCHNELL S, MAINI PK. Formation of vertebral precursors: past models and future predictions. J. Theor. Med. 2003;5:23–35.
-
- BAKER RE, SCHNELL S, MAINI PK. A clock and wavefront mechanism for somite formation. Dev. Biol. 2006a;293:116–126. - PubMed

