Confidence intervals for fitting of atomic models into low-resolution densities
- PMID: 19564688
- PMCID: PMC2703574
- DOI: 10.1107/S0907444909012876
Confidence intervals for fitting of atomic models into low-resolution densities
Abstract
The fitting of high-resolution structures into low-resolution densities obtained from techniques such as electron microscopy or small-angle X-ray scattering can yield powerful new insights. While several algorithms for achieving optimal fits have recently been developed, relatively little effort has been devoted to developing objective measures for judging the quality of the resulting fits, in particular with regard to the danger of overfitting. Here, a general method is presented for obtaining confidence intervals for atomic coordinates resulting from fitting of atomic resolution domain structures into low-resolution densities using well established statistical tools. It is demonstrated that the resulting confidence intervals are sufficiently accurate to allow meaningful statistical tests and to provide tools for detecting potential overfitting.
Figures
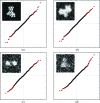

Similar articles
-
The joys and perils of flexible fitting.Adv Exp Med Biol. 2014;805:137-55. doi: 10.1007/978-3-319-02970-2_6. Adv Exp Med Biol. 2014. PMID: 24446360
-
Structure of human rhinovirus complexed with Fab fragments from a neutralizing antibody.J Virol. 1993 Mar;67(3):1148-58. doi: 10.1128/JVI.67.3.1148-1158.1993. J Virol. 1993. PMID: 7679742 Free PMC article.
-
Structure determination of an Fab fragment that neutralizes human rhinovirus 14 and analysis of the Fab-virus complex.J Mol Biol. 1994 Jul 8;240(2):127-37. doi: 10.1006/jmbi.1994.1427. J Mol Biol. 1994. PMID: 8027997
-
Structural characterization of proteins and complexes using small-angle X-ray solution scattering.J Struct Biol. 2010 Oct;172(1):128-41. doi: 10.1016/j.jsb.2010.06.012. Epub 2010 Jun 15. J Struct Biol. 2010. PMID: 20558299 Review.
-
Refinement of Atomic Structures Against cryo-EM Maps.Methods Enzymol. 2016;579:277-305. doi: 10.1016/bs.mie.2016.05.033. Epub 2016 Jun 24. Methods Enzymol. 2016. PMID: 27572731 Review.
Cited by
-
Three-Dimensional Structures of Full-Length, Membrane-Embedded Human α(IIb)β(3) Integrin Complexes.Biophys J. 2016 Feb 23;110(4):798-809. doi: 10.1016/j.bpj.2016.01.016. Biophys J. 2016. PMID: 26910421 Free PMC article.
-
Macromolecular refinement of X-ray and cryoelectron microscopy structures with Phenix/OPLS3e for improved structure and ligand quality.Structure. 2021 Aug 5;29(8):913-921.e4. doi: 10.1016/j.str.2021.03.011. Epub 2021 Apr 5. Structure. 2021. PMID: 33823127 Free PMC article.
-
New tools for the analysis and validation of cryo-EM maps and atomic models.Acta Crystallogr D Struct Biol. 2018 Sep 1;74(Pt 9):814-840. doi: 10.1107/S2059798318009324. Epub 2018 Sep 3. Acta Crystallogr D Struct Biol. 2018. PMID: 30198894 Free PMC article.
-
Future prospects.Adv Protein Chem Struct Biol. 2011;82:101-21. doi: 10.1016/B978-0-12-386507-6.00005-1. Adv Protein Chem Struct Biol. 2011. PMID: 21501821 Free PMC article. Review.
-
Validation methods for low-resolution fitting of atomic structures to electron microscopy data.Arch Biochem Biophys. 2015 Sep 1;581:49-53. doi: 10.1016/j.abb.2015.06.017. Epub 2015 Jun 24. Arch Biochem Biophys. 2015. PMID: 26116787 Free PMC article.
References
-
- Anderson, T. W. & Darling, D. A. (1952). Ann. Math. Stat.23, 193–212.
-
- Baker, T. S. & Johnson, J. E. (1996). Curr. Opin. Struct. Biol.6, 585–594. - PubMed
-
- Böttcher, B., Wynne, S. A. & Crowther, R. A. (1997). Nature (London), 386, 88–91. - PubMed
-
- Britton, K. L., Baker, P. J., Rice, D. W. & Stillman, T. J. (1992). Eur. J. Biochem.209, 851–859. - PubMed
-
- Brünger, A. T. (1992). Nature (London), 355, 472–475. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

