Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2011:62:583-619.
doi: 10.1146/annurev.psych.093008.100356.

The disaggregation of within-person and between-person effects in longitudinal models of change

Patrick J Curran  1 , Daniel J Bauer
Affiliations
Review

The disaggregation of within-person and between-person effects in longitudinal models of change

Patrick J Curran et al. Annu Rev Psychol. 2011.

Abstract

Longitudinal models are becoming increasingly prevalent in the behavioral sciences, with key advantages including increased power, more comprehensive measurement, and establishment of temporal precedence. One particularly salient strength offered by longitudinal data is the ability to disaggregate between-person and within-person effects in the regression of an outcome on a time-varying covariate. However, the ability to disaggregate these effects has not been fully capitalized upon in many social science research applications. Two likely reasons for this omission are the general lack of discussion of disaggregating effects in the substantive literature and the need to overcome several remaining analytic challenges that limit existing quantitative methods used to isolate these effects in practice. This review explores both substantive and quantitative issues related to the disaggregation of effects over time, with a particular emphasis placed on the multilevel model. Existing analytic methods are reviewed, a general approach to the problem is proposed, and both the existing and proposed methods are demonstrated using several artificial data sets. Potential limitations and directions for future research are discussed, and recommendations for the disaggregation of effects in practice are offered.

PubMed Disclaimer

Figures

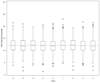
Figure 1
Figure 1
The time-specific distributions of the TVC (zti) for the first artificial data set.
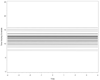
Figure 2
Figure 2
Model-implied growth trajectories for the TVC (zti) over time for 50 randomly drawn observations from the first artificial data set.
Figure 3
Figure 3
The time-specific values of the TVC over time for a randomly drawn case from the first artificial data set.
Figure 4
Figure 4
The bivariate distribution between the outcome (i.e., yti) and the time-varying covariate (i.e., zti).
Figure 5
Figure 5
The bivariate distribution between the outcome (yti) and the person-mean centered time-varying covariate (żti).
Figure 6
Figure 6
The bivariate distribution between the person-mean of the outcome (ȳi) and the person-mean of the time-varying covariate (z̄i).
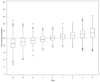
Figure 7
Figure 7
The time-specific distributions of the TVC (zti) for the second artificial data set.
Figure 8
Figure 8
Model-implied growth trajectories for the TVC (i.e., zti) over time for 50 randomly drawn observations from the second artificial data set.
Figure 9
Figure 9
The time-specific values of the TVC over time for a randomly drawn case from the second artificial data set.
Figure 10
Figure 10
Model-implied growth trajectories for the TVC (i.e., zti) over time for 50 randomly drawn observations from the third artificial data set.
Figure 11
Figure 11
The cohort-specific distributions of the person-means of the time-varying covariate (i.e., z̄i) pooling over time and within cohort for the third artificial data set.
See this image and copyright information in PMC

References

    1. Aiken LS, West SG. Multiple Regression: Testing and Interpreting Interactions. Newbury Park, CA: Sage; 1991.
    1. Bauer DJ. Estimating multilevel linear models as structural equation models. J. Educ. Behav. Stat. 2003;28:135–167.
    1. Biesanz JC, Deeb-Sossa N, Aubrecht AM, Bollen KA, Curran PJ. The role of coding time in estimating and interpreting growth curve models. Psychol. Methods. 2004;9:30–52. - PubMed
    1. Bollen KA, Curran PJ. Autoregressive latent trajectory (ALT) models: a synthesis of two traditions. Sociol. Methods Res. 2003;32:336–383.
    1. Bollen KA, Curran PJ. Latent Curve Models: A Structural Equation Approach. Wiley Series on Probability and Mathematical Statistics. Hoboken, NJ: Wiley-Intersci; 2006.

Publication types