A compact representation of drawing movements with sequences of parabolic primitives
- PMID: 19578429
- PMCID: PMC2699652
- DOI: 10.1371/journal.pcbi.1000427
A compact representation of drawing movements with sequences of parabolic primitives
Abstract
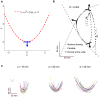
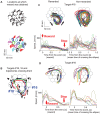
Some studies suggest that complex arm movements in humans and monkeys may optimize several objective functions, while others claim that arm movements satisfy geometric constraints and are composed of elementary components. However, the ability to unify different constraints has remained an open question. The criterion for a maximally smooth (minimizing jerk) motion is satisfied for parabolic trajectories having constant equi-affine speed, which thus comply with the geometric constraint known as the two-thirds power law. Here we empirically test the hypothesis that parabolic segments provide a compact representation of spontaneous drawing movements. Monkey scribblings performed during a period of practice were recorded. Practiced hand paths could be approximated well by relatively long parabolic segments. Following practice, the orientations and spatial locations of the fitted parabolic segments could be drawn from only 2-4 clusters, and there was less discrepancy between the fitted parabolic segments and the executed paths. This enabled us to show that well-practiced spontaneous scribbling movements can be represented as sequences ("words") of a small number of elementary parabolic primitives ("letters"). A movement primitive can be defined as a movement entity that cannot be intentionally stopped before its completion. We found that in a well-trained monkey a movement was usually decelerated after receiving a reward, but it stopped only after the completion of a sequence composed of several parabolic segments. Piece-wise parabolic segments can be generated by applying affine geometric transformations to a single parabolic template. Thus, complex movements might be constructed by applying sequences of suitable geometric transformations to a few templates. Our findings therefore suggest that the motor system aims at achieving more parsimonious internal representations through practice, that parabolas serve as geometric primitives and that non-Euclidean variables are employed in internal movement representations (due to the special role of parabolas in equi-affine geometry).
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

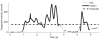
 .
.




Similar articles
-
Parabolic movement primitives and cortical states: merging optimality with geometric invariance.Biol Cybern. 2009 Feb;100(2):159-84. doi: 10.1007/s00422-008-0287-0. Epub 2009 Jan 17. Biol Cybern. 2009. PMID: 19152065
-
Affine differential geometry analysis of human arm movements.Biol Cybern. 2007 Jun;96(6):577-601. doi: 10.1007/s00422-007-0145-5. Epub 2007 Apr 4. Biol Cybern. 2007. PMID: 17406889 Free PMC article.
-
Affine differential geometry and smoothness maximization as tools for identifying geometric movement primitives.Biol Cybern. 2017 Feb;111(1):5-24. doi: 10.1007/s00422-016-0705-7. Epub 2016 Nov 7. Biol Cybern. 2017. PMID: 27822891
-
Role of the Cerebellum in the Construction of Functional and Geometrical Spaces.Cerebellum. 2024 Dec;23(6):2538-2563. doi: 10.1007/s12311-024-01693-y. Epub 2024 Apr 16. Cerebellum. 2024. PMID: 38625534 Review.
-
Motor primitives in vertebrates and invertebrates.Curr Opin Neurobiol. 2005 Dec;15(6):660-6. doi: 10.1016/j.conb.2005.10.011. Epub 2005 Nov 4. Curr Opin Neurobiol. 2005. PMID: 16275056 Review.
Cited by
-
"Biological geometry perception": visual discrimination of eccentricity is related to individual motor preferences.PLoS One. 2011 Jan 19;6(1):e15995. doi: 10.1371/journal.pone.0015995. PLoS One. 2011. PMID: 21283813 Free PMC article.
-
Complex Upper-Limb Movements Are Generated by Combining Motor Primitives that Scale with the Movement Size.Sci Rep. 2018 Aug 27;8(1):12918. doi: 10.1038/s41598-018-29470-y. Sci Rep. 2018. PMID: 30150687 Free PMC article.
-
Spatiomotor dynamics of hand movements during the drawing of memory-guided trajectories without visual feedback.J Neurophysiol. 2025 Jun 1;133(6):1665-1674. doi: 10.1152/jn.00153.2024. Epub 2025 Apr 2. J Neurophysiol. 2025. PMID: 40172920 Free PMC article.
-
Arm trajectories and writing strategy in healthy children.BMC Pediatr. 2012 Nov 7;12:173. doi: 10.1186/1471-2431-12-173. BMC Pediatr. 2012. PMID: 23134839 Free PMC article.
-
Learning not to generalize: modular adaptation of visuomotor gain.J Neurophysiol. 2010 Jun;103(6):2938-52. doi: 10.1152/jn.01089.2009. Epub 2010 Mar 31. J Neurophysiol. 2010. PMID: 20357068 Free PMC article.
References
-
- Todorov E, Jordan MI. Smoothness maximization along a predefined path accurately predicts the speed profiles of complex arm movements. J Neurophysiol. 1998;80:696–714. - PubMed
-
- Uno Y, Kawato M, Suzuki R. Formation and control of optimal trajectory in human multijoint arm movement. Minimum torque-change model. Biol Cybern. 1989;61:89–101. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

